LA CONSERVACIÓN DE LA ENERGÍA MECÁNICA
CONCEPTOS BÁSICOS DE LA CONSERVACIÓN DE LA ENERGÍA MECÁNICA
Si un objeto lo dejamos caer desde una altura “h”, podemos calcular el trabajo (W) que realiza la fuerza gravitacional como la diferencia de las energías potenciales.
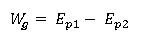
Si ya sabemos por el teorema de Trabajo-energía que el trabajo total aplicado a un objeto es igual al cambio de sus energías cinéticas, podemos obtener:
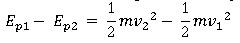
Colocando las variables de posición inicial de un lado y las variables de la posición final del otro, obtenemos
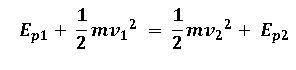
DEFINICIÓN DE LA ENERGÍA MECÁNICA TOTAL DE UN CUERPO
La energía mecánica total de un cuerpo es la suma de la energía cinética más la energía potencial de ese cuerpo.
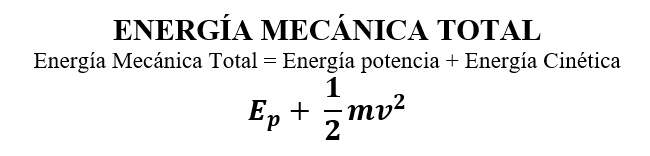
Como vemos, la energía mecánica total de un cuerpo en una posición 1, es igual a la energía mecánica total de ese cuerpo en la posición 2.
A este principio se le conoce como “La conservación de la energía mecánica”.
TEOREMA DE LA CONSERVACIÓN DE LA ENERGÍA MECÁNICA
El teorema de la conservación de la energía mecánica nos dice que la suma de la energía potencia y cinética del estado de movimiento de un cuerpo es igual a la suma de esas mismas energías de otro estado de movimiento de ese mismo cuerpo.
Es decir, lo que varía entre un estado de movimiento a otro, es la cantidad relativa de energía potencial o de energía cinética que tiene el cuerpo. En un estado puede tener mayor energía potencial que cinética, y en el otro puede tener mayor energía cinética, pero la suma de las dos energías es la misma.
FORMULA DE LA CONSERVACIÓN DE LA ENERGÍA MECÁNICA
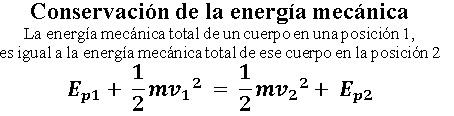
EJEMPLOS:
1.- Una pelota de 2 kg se deja caer de un edificio. Cuando la pelota está a 5 metros del piso, esta tiene una velocidad de 20 m/s. Determina su energía mecánica en ese punto.
Primero determinamos la formula a utilizar:
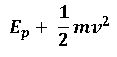
Después sustituimos nuestros datos:
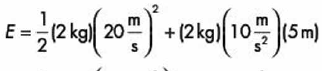
Realizamos las operaciones y obtenemos:
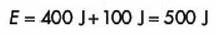
LA LEY DE LA CONSERVACIÓN DE LA ENERGÍA
El análisis anterior solo se aplica para energía conservativas, es decir para la energía mecánica que se conserva, que como ya definimos, es igual a la energía cinética más la energía potencial.
Sin embargo, en la mayoría de los movimientos, se interacciona con otras fuerzas, tales como la fricción. A pesar de esto, si se considera a el calor generado por la fricción como una energía interna y la agregamos en nuestra ecuación de la conservación de la energía mecánica, obtenemos que:
El cambio de la energía cinética, más el cambio en la energía potencia más el cambio en la energía interna es igual a cero.
Es decir, el cambio en la energía total del sistema siempre es cero. Si una energía aumenta, tiene que disminuir la otra y viceversa.
Esta ecuación es la forma general de “La ley de la conservación de la energía”
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM de Física Área 4-2023$90.00
Guía UNAM de Física Área 4-2023$90.00 -
 Guía UNAM de Física Área 3-2023$90.00
Guía UNAM de Física Área 3-2023$90.00 -
 Guía UNAM de Física Área 2-2023$90.00
Guía UNAM de Física Área 2-2023$90.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00 -
 Guía UNAM de Física Área 1-2023$90.00
Guía UNAM de Física Área 1-2023$90.00




buenas tardes, tengo una pregunta con respecto al ejercicio del ejemplo. Podrían explicarme de donde proviene la cantidad de ( 10 m/s²)
Claro. Es la aceleración de la fuerza de gravedad de la Tierra (9.8 m/s2) pero en algunos casos se redondea 10, para facilitar las operaciones.