ECUACIONES DE LAS MEDIANAS, MEDIATRICES, Y ALTURAS DE UN TRIÁNGULO. PUNTOS DE INTERSECCIÓN (ORTOCENTRO, CIRCUNCENTRO Y BARICENTRO)
Este tema es el uso de todas las herramientas aprendidas sobre la recta para resolver un tipo especial de problemas en las líneas de los triángulos.
Se requiere:
1.- Saber utilizar los conceptos de capítulos anteriores:
Diferentes formas de la ecuación de la recta
División de segmentos de la recta
Paralelismo y perpendicularidad en la recta
2.- Conocer las definiciones de las rectas de los triángulos
Mediana
Mediatriz
Altura
Baricentro
Circuncentro
Ortocentro
DEFINICIONES Y PROCEDIMIENTOS:
MEDIANA:
La mediana es el segmento de recta que une un vértice del triángulo con el punto medio del lado opuesto.
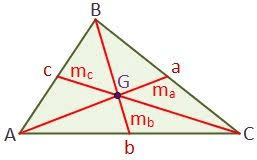
PROCEDIMIENTO PARA OBTENER LA ECUACIÓN DE LA MEDIANA:
1-Se utiliza la ecuación de la recta que pasa por 2 puntos
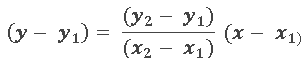
2.-En esta ecuación se sustituye (x1, y1) por el vértice desde donde se vaya a tomar la mediana.
3.-Para obtener el otro punto (x2, y2) se obtiene a partir de la fórmula para el punto medio de una recta.

En este caso, (x1, y1), (x2, y2) serán los valores del lado opuesto al vértice donde salga la mediana
MEDIATRIZ:
La mediatriz es la recta que pasa por el punto medio de un lado de un triángulo y que es perpendicular a ese mismo lado.
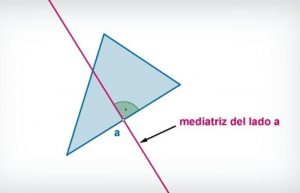
PROCEDIMIENTO PARA OBTENER LA ECUACIÓN DE LA MEDIATRIZ:
1-Se utiliza la ecuación de la recta punto-pendiente
y – y1 = m (x – x1)
2.-En esta ecuación se sustituye (x1, y1) por el punto medio del lado donde se vaya a tomar la mediatriz, ocupando las fórmulas para el punto medio:

3.-Para obtener la pendiente m, se calcula la pendiente de este mismo lado y se aplica la perpendicularidad de las líneas.
m1 = – (1/ m2) o m1 + m2 = -1
ALTURA:
Es el segmento de recta perpendicular trazado desde un vértice del triángulo hacia el lado opuesto.
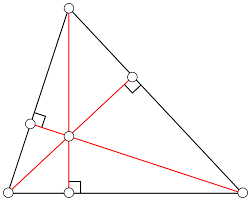
PROCEDIMIENTO PARA OBTENER LA ECUACIÓN DE LA ALTURA:
1-Se utiliza la ecuación de la recta punto-pendiente
y – y1 = m (x – x1)
2.-En esta ecuación se sustituye (x1, y1) por el vértice desde donde se vaya a tomar la altura.
3.-Para obtener la pendiente m, se calcula la pendiente del lado opuesto al vértice anterior y se aplica la perpendicularidad de las líneas.
m1 = – (1/ m2) o m1 + m2 = -1
PUNTOS DE INTERSECCIÓN EN UN TRIANGULO:
BARICENTRO:
Es el punto donde se interceptan las medianas
Para obtener sus coordenadas, utilizamos la formula siguiente:
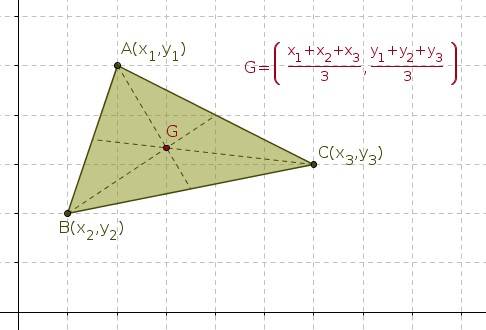
CIRCUNCENTRO:
El circuncentro es el punto donde se interceptan las mediatrices.
También se llama circuncentro, porque si trazamos un círculo que toque los vértices del triángulo en cuestión, el circuncentro, será el centro del círculo trazado.
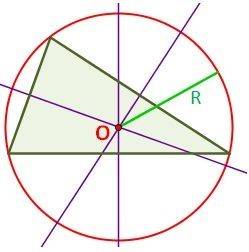
Para hallar las coordenadas del circuncentro:
1.-Se deben obtener las ecuaciones de dos de las mediatrices
2.-Con esto se resuelve el sistema de dos ecuaciones con 2 incógnitas para obtener el punto en el que se interceptan, el cual será el circuncentro del triangulo
ORTOCENTRO:
El ortocentro es el punto donde se interceptan las alturas
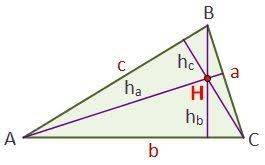
Para hallar las coordenadas del ortocentro:
1.-Se deben obtener las ecuaciones de dos de las alturas
2.-Con esto se resuelve el sistema de dos ecuaciones con 2 incógnitas para obtener el punto en el que se interceptan, el cual será el ortocentro del triangulo
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00







