FORMAS ORDINARIA (CANÓNICA) Y GENERAL DE LA ECUACIÓN DE LA CIRCUNFERENCIA CON CENTRO EN EL ORIGEN
Las formas ordinaria y general de la ecuación de la circunferencia con centro en el origen son las siguientes.
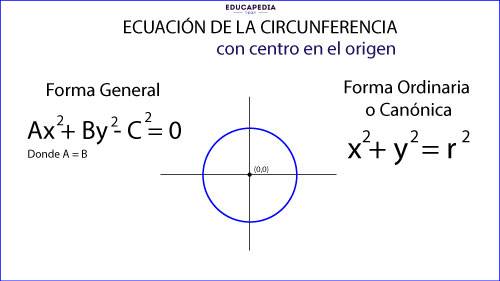
ECUACIÓN ORDINARIA DE LA CIRCUNFERENCIA CON CENTRO EN EL ORIGEN

ECUACIÓN GENERAL DE LA CIRCUNFERENCIA CON CENTRO EN EL ORIGEN

¡IMPORTANTE!
Para poder entender e interpretar los datos de las formas de la ecuación de la circunferencia es importante que sepas como se generan estas formas.
ORIGEN LA ECUACIÓN DE LA CIRCUNFERENCIA
Si trazamos la circunferencia en el plano cartesiano, podemos trazar un triángulo rectángulo con “r” como la distancia entre cualquier punto al centro como hipotenusa.
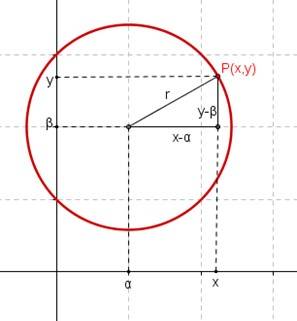
A esto le aplicamos el teorema de Pitágoras:
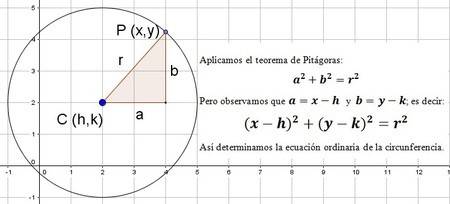
Con esto obtenemos,la forma ordinaria de la circunferencia con centro en (h, k).
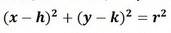
En el caso de que el centro esté en el origen, la forma ordinaria de la ecuación será:
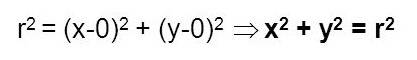
Ejemplos de la forma ordinaria y general de la ecuación de la circunferencia con centro en el origen
1.- Identifica cuál de las siguientes ecuaciones representan a una circunferencia:

Debido a que todas las ecuaciones anteriores excepto la opción c infringen el criterio de que para representar a una circunferencia los coeficientes de las variables deben de ser idénticos (número y signo). Por lo tanto, la opción correcta es “c”
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00