TEOREMAS QUE JUSTIFICAN LAS PROPIEDADES DE LA INTEGRAL DE UNA FUNCIÓN

PRIMER TEOREMA FUNDAMENTAL DEL CALCULO

---

El primer teorema fundamental del cálculo es aquel que demuestra que la derivación y la integración de una función, son operaciones inversas.

“Si f(x) es continua en [a, b] entonces F(x), su función integral es derivable y F´(x) = f(x)”.

Es decir, la función F(x) que se obtiene de integrar una función original f(x) se puede derivar y su derivada es la misma función original.  De forma parecida a que obtuviera el cuadrado de un numero x² y luego le aplicas raíz cuadrada √x². Te dará el mismo número original.

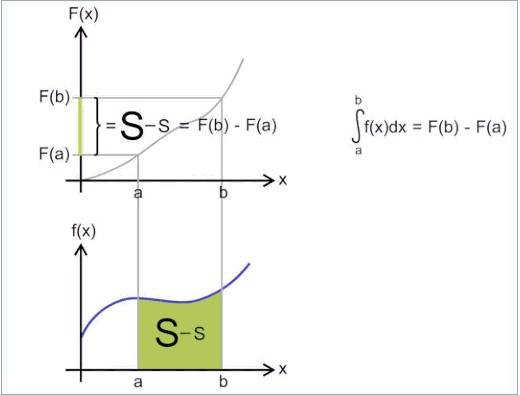
SEGUNDO TEOREMA FUNDAMENTAL DEL CALCULO

---

Dada f(x) una función continua en [a, b], P(x) una primitiva de f(x) en [a, b] y F(x) una función integral de f(x) tenemos que:

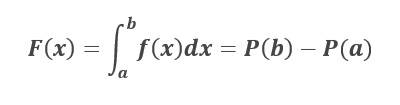
TEOREMA DEL VALOR MEDIO DEL CALCULO INTEGRAL

---

Dada una funciona continua en [a, b], existe al menos un c ϵ (a, b) tal que:

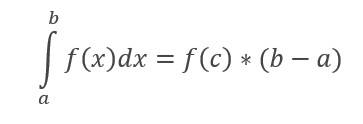
PROPIEDADES DE LA INTEGRAL DE UNA FUNCIÓN

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.