DEFINICIÓN DE DERIVADA Y SUS NOTACIONES
DEFINICIÓN DE DERIVADA
“La derivada de una función es la razón de cambio instantánea con la que varía el valor de una función según se modifique el valor de su variable independiente”.
Es decir, es el cambio que hay entre dos valores de “y” (f(x1) y f (x2)) cuando hay un cambio extremadamente pequeño de la variable independiente “x” (que se expresa como (x2 – x1) tiende a cero y que se considera por ser extremadamente pequeño como un solo punto (x).
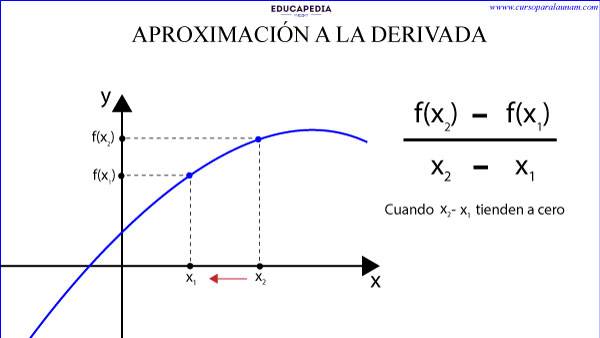
LA DERIVADA EN TÉRMINOS FORMALES DE LIMITES SE EXPRESA COMO:
La derivada es el límite de la diferencia de cambio de f(x), expresado como (f (x + Δx) – f(x)); entre el incremento de x, expresado como (Δx); cuando este incremento tiende a cero.
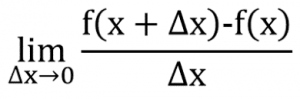
Es decir, la derivada nos va a decir en qué proporción cambia el valor de “y”, cada vez que cambiamos “x” en cambios infinitesimalmente pequeños.
OTRA NOTACIÓN CON LIMITES:
El cambio de x, también se puede expresar como: x2 – x1 = Δx = h de tal manera que la derivada también se puede expresar en términos de “h”.
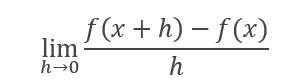
NOTACIONES DE LA DERIVADA:
Las diferentes notaciones que podemos ocupar para representar la derivada de una función son:

OBTENCIÓN DE LA DERIVADA UTILIZANDO LIMITES
Recordemos que la definición de derivada utilizando limites es:
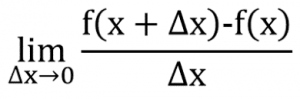
Por lo tanto, para obtener la derivada de una función utilizando limites, simplemente tenemos que sustituir la función dada en la definición de derivada.
Ejemplos de la derivada y sus notaciones:
1.- Calcula la derivada de la siguiente función utilizando su definición en términos de límites:
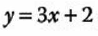
Sustituyendo en nuestra definición obtenemos:
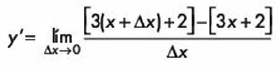
Simplificando obtenemos la derivada de nuestra función:
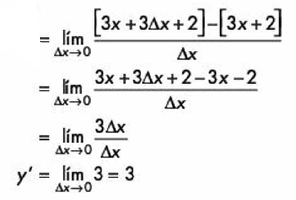
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00








Los comentarios están cerrados.