MOVIMIENTO UNIFORMEMENTE ACELERADO
CONCEPTOS BÁSICOS DEL MOVIMIENTO UNIFORMEMENTE ACELERADO (M. U. A.)
MOVIMIENTO UNIFORMEMENTE ACELERADO:
El movimiento uniformemente acelerado (m. u. a.) es aquel donde los cuerpos se mueven en línea recta con una aceleración constante.
Es decir, sí cambia la velocidad, pero lo hace a una tasa constante, si aumenta la velocidad, en cada lapso de tiempo aumenta la misma cantidad y si disminuye lo hace de la misma forma.
¡Recuerda!
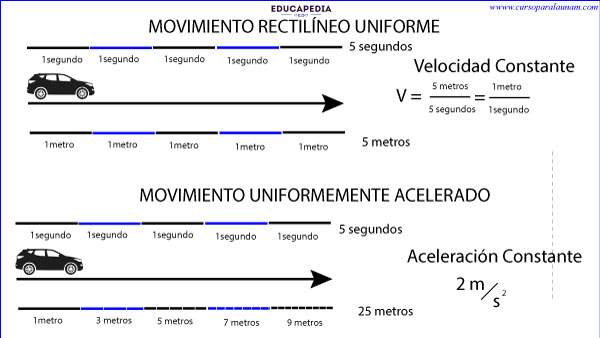
En el movimiento rectilíneo uniforme, la velocidad es constante, en este movimiento, la aceleración es constante, es decir, el cambio en la velocidad es constante.
Como ya habíamos definido la velocidad constante como una tasa “constante”, de cambio de posición con respecto al tiempo.
La Aceleración Constante también es una tasa constante, pero de cambio de velocidad con respecto al tiempo, es decir, para cada misma magnitud de velocidad que se incrementa, le corresponde una misma magnitud de tiempo que se incrementa.
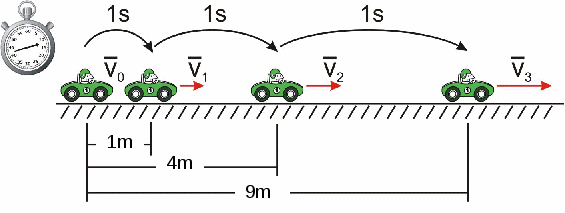
LA ACELERACIÓN CONTANTE EN TÉRMINOS DE LA POSICIÓN:
La aceleración contante la podemos definir como la tasa variable de cambio de posición con respecto al tiempo.
Es decir, a cada segmento de tiempo idéntico, tiene un recorrido más amplio o más corto que los demás.
OTROS EJEMPLOS DE MOVIMIENTO UNIFORMEMENTE ACELERADO:
-La fruta que cae de un árbol, acelerada por la fuerza de gravedad.
-Una pelota que es lanzada hacia arriba que es desacelerada por la fuerza de la gravedad.
-Un auto que parte del reposo y alcanza cierta velocidad de movimiento
PRINCIPALES TIPOS DE MOVIMIENTO UNIFORMEMENTE ACELERADO
1.-Movimiento rectilíneo uniformemente acelerado
1.1 Horizontal (acelerado)
1.2 Vertical o Caída Libre
1.3 Tiro vertical (ascendente y descendente)
2.- Tiro parabólico
3.-Movimiento circular
1.-MOVIMIENTO RECTILÍNEO UNIFORMEMENTE ACELERADO (m.r.u.a)

El movimiento rectilíneo uniformemente acelerado es el movimiento que cambia de velocidad a una tasa constante sobre una línea recta.
TIPOS DE MOVIMIENTO RECTILÍNEO UNIFORMEMENTE ACELERADO
Los tipos de movimiento rectilíneo uniformemente acelerado pueden ser:
1.- Horizontal: Como la trayectoria de un coche
2.- Vertical: Como la caída de los cuerpos
MOVIMIENTO RECTILÍNEO UNIFORMEMENTE ACELERADO HORIZONTAL
VELOCIDAD MEDIA:
Para obtener la velocidad media de los cuerpos que viajan en línea recta con una aceleración uniforme se pueden ocupar las siguientes formulas:
1era fórmula de la velocidad media del M.R.U.A: La velocidad media del M.R.U.A es igual a la distancia recorrida entre el tiempo transcurrido.
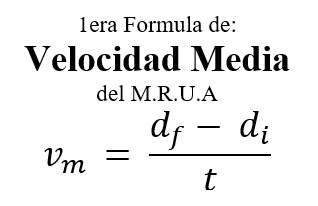
2da fórmula de la velocidad media del M.R.U.A: La velocidad media del M.R.U.A es igual al promedio de las velocidades utilizadas en el recorrido.

ACELERACIÓN MEDIA DEL M.R.U.A.:
La aceleración media es el cambio promedio de la velocidad de un cuerpo con respecto al tiempo total.
Es decir, la aceleración media es igual a la diferencia de las velocidades (la final menos la inicial) entre el tiempo transcurrido.

Ejemplos:
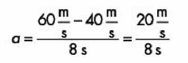
1.- Un auto se mueve a una velocidad de 40 m/s, después acelera durante 8 segundo hasta alcanzar la velocidad de 60 m/s. Calcula la aceleración que tuvo en ese lapso de 8 segundo.
Primero determinamos la fórmula que vamos a utilizar:
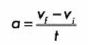
Después realizamos la sustitución de nuestros datos:
Realizamos las operaciones y obtenemos:
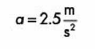
CUERPO EN CAIDA LIBRE

CONCEPTOS BÁSICOS DE CAÍDA LIBRE
Los cuerpos en caída libre son los movimientos de los objetos que caen debido al efecto de la atracción gravitacional hacia el centro de la Tierra.
El análisis de estos movimientos es el mismo que para el movimiento rectilíneo uniformemente acelerado, con la excepción que consideramos la aceleración constante con un valor de 9.81 m/s2.
CONSIDERACIONES PARA PASAR DEL M. R. U. A. AL DE CAÍDA LIBRE:
1.- Consideramos a la distancia inicial y la velocidad inicial, igual a cero
2.- Sustituimos a la “a” (aceleración) por “g” (aceleración de la aceleración gravitacional).
3.- Y consideramos a la distancia recorrida como “h” (altura recorrida).
Con esto, las fórmulas del movimiento rectilíneo uniformemente acelerado quedan para la caída libre de la siguiente forma:
FORMULAS PARA LOS CUERPOS EN CAÍDA LIBRE:




Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
TIRO VERTICAL (ascendente y descendente)

CONSIDERACIONES PARA PASAR del M.R.U.A AL DE TIRO VERTICAL:
1.- En el lanzamiento de los cuerpos hacia arriba, se considera a la aceleración como negativa (o también llamada desaceleración).
2.- En el movimiento descendente (movimiento hacia abajo) la aceleración se considera positiva
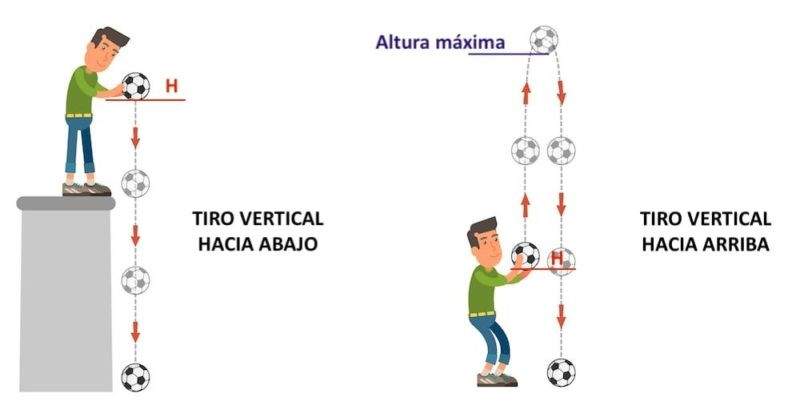
“El análisis de estos movimientos es el mismo que para el movimiento rectilíneo uniformemente acelerado, con la excepción que consideramos la aceleración con un valor de -9.81 m/s2 para el movimiento ascendente porque desacelera la velocidad inicial y un valor de 9. 81 m/s2 para el movimiento descendente porque acelera el movimiento de caída libre”.
FORMULAS PARA EL TIRO VERTICAL (ASCENDENTE Y DESCENDENTE)



Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
TIRO PARABOLICO

El tiro parabólico representa el lanzamiento de los cuerpos hacia el frente y hacia arriba, lo que provoca un movimiento con forma parabólica debido a la velocidad inicial y a la atracción gravitacional hacia abajo.
Por un lado, tienen una trayectoria horizontal donde el móvil se desplaza de un lado hacia el otro, y por el otro lado, tiene una trayectoria vertical donde sube y luego baja.
CARACTERÍSTICAS DEL TIRO PARABÓLICO
1.- La componente horizontal de la velocidad es constante
2.- La componente vertical de la velocidad es variable, debido al efecto de la aceleración gravitacional.
3.- La componente vertical de la velocidad en el punto más alto, es igual a cero.
FORMULAS PARA EL TIRO PARABÓLICO
Gracias a que la trayectoria y la velocidad se pueden estudiar a través de sus componentes, el componente horizontal (x) y el componente vertical (y).





“La magnitud de la velocidad con la que impacta al caer a la superficie es igual a la magnitud de la velocidad inicial. (considerando que la superficie es totalmente horizontal)”.
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
MOVIMIENTO CIRCULAR

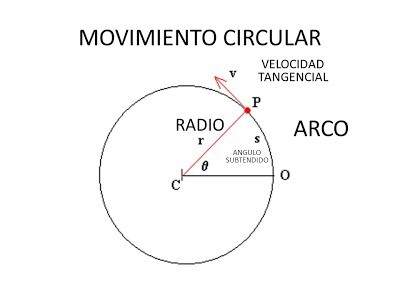
El movimiento circular uniforme de un cuerpo es aquel que tiene una trayectoria en forma de circunferencia, es decir, gira alrededor de un eje y tiene un radio constante, adema gira con una rapidez constante.
CONCEPTOS BÁSICOS DEL MOVIMIENTOS CIRCULAR UNIFORME
¿Por qué un cuerpo que se mueve en forma circular con una rapidez constante tiene una aceleración diferente de cero?
Incluso aunque nos parezca contra intuitiva esta pregunta, el problema radica en la idea común de que velocidad es lo mismo que rapidez.
La rapidez es una cantidad escalar que expresa la tasa de cambio de posición con respecto al tiempo.
La velocidad es un vector, compuesto por una magnitud escalar y una dirección.
Por lo tanto, la velocidad expresa la tasa de cambio de su posición con respecto al tiempo, pero TAMBIÉN, la tasa de cambio de la DIRECCIÓN de la posición del cuerpo.
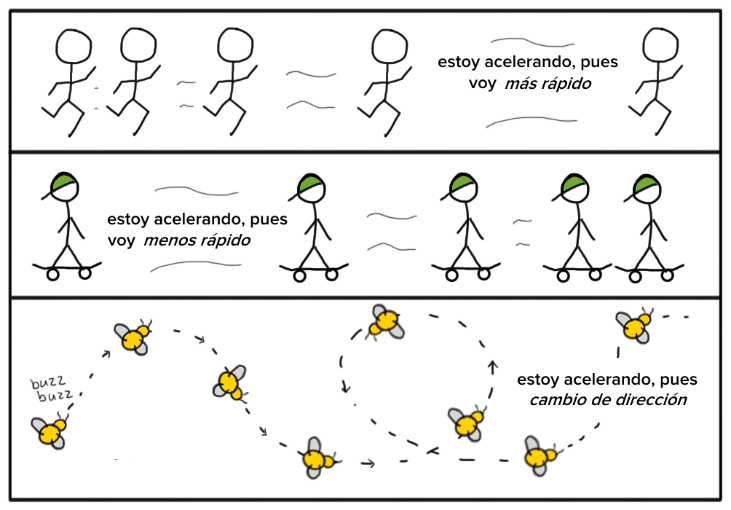
En los temas anteriores hemos considerado la rapidez y la velocidad como sinónimos porque “no hay cambio en la dirección”.
Si un cuerpo va por un camino ondulado con una rapidez constante, su rapidez será CONSTANTE, pero su velocidad irá cambiando, porque la dirección de esa rapidez va cambiando.
ACELERACIÓN DEL MOVIMIENTO CIRCULAR UNIFORME
Por lo tanto, si su velocidad va cambiando, TENDRÁ UNA ACELERACIÓN.
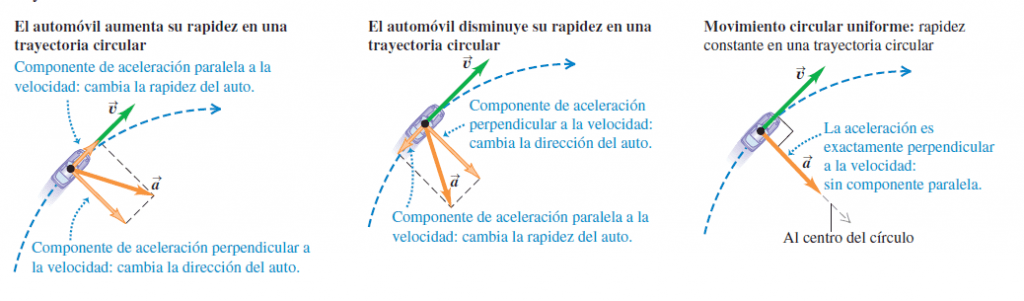
Esta aceleración tendrá 2 componentes, una paralela a la rapidez y otra perpendicular.
La componente paralela a la rapidez es cero si la rapidez es constante (movimiento circular uniforme) pero si la rapidez varia, entonces esta componente será diferente de cero.
La componente de la perpendicular será siempre diferente de cero para este tipo de movimiento porque siempre está cambiando la dirección de la velocidad.
MOVIMIENTO PERIODICO U OSCILACION

El movimiento periódico u oscilatoria es aquel movimiento que va y viene entre un mismo segmento de desplazamiento.
Es decir, tiene una posición de equilibrio estable y cuando se le aleja de esta posición y se le suelta, entra en acción una fuerza para regresarlo al equilibrio.
Sin embargo, cuando regresa al equilibrio ya ha adquirido cierta energía cinética que le lleva a la posición contraria y vuelve a tratar de regresar al equilibrio, lo que le lleva a repetir el movimiento.
CONCEPTOS BÁSICO DEL MOVIMIENTO PERIÓDICO:
Amplitud (A): Es la magnitud máxima de desplazamiento con respecto al equilibrio.
El periodo (T): es el tiempo que tarda un ciclo.
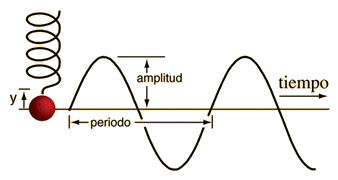
Ciclo o vibración completa: Es un viaje redondo de ida y vuelta, primero hacia un lado de equilibrio y su regreso, y después hacia el otro lado del equilibrio y su regreso al equilibrio.
La frecuencia (f): Es el número de ciclos en una unidad de tiempo.
La frecuencia se mide en Hertz (sistema SI):
1 Hertz = 1 ciclo/segundo.
El periodo es el reciproco de la frecuencia
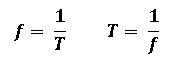
MOVIMIENTO ARMÓNICO SIMPLE (MAS)

El movimiento armónico simple (MAS) es un tipo de movimiento oscilatorio donde la fuerza de restitución es directamente proporcional al desplazamiento con respecto al equilibrio.
Es decir, entre más grande sea el desplazamiento inicial más grande será la fuerza que intenta regresarlo a su punto de equilibrio.
El ejemplo más común de este tipo de movimiento son los resortes. Entre mas estiras un resorte, habrá una fuerza mayor para que regrese a su posición de equilibrio.
También podemos decir que el MAS:
Es cuando un objeto vibra baja la acción de fuerzas restauradoras a una posición de equilibrio y que son proporcionales a la distancia a este equilibrio.
Al cuerpo que tiene un movimiento armónico simple se le llama “oscilador armónico”.
La característica más importante del movimiento armónico simple es que cumple con la Ley de Hooke (Ley de un resorte), la cual es la siguiente.
Fx = -kx
Fx = la fuerza de restitución del cuerpo
x = desplazamiento del cuerpo
-k = constante elástica
FORMULA PARA OBTENER LA FUERZA SOBRE UN CUERPO DEL MOVIMIENTO ARMÓNICO SIMPLE

ENERGÍA MECÁNICA TOTAL DEL MOVIMIENTO ARMÓNICO SIMPLE

Debido a que cuando el objeto se estira su máxima amplitud (A), la v = 0, toda la energía será potencial en ese punto, y además por el mismo principio de conservación de la energía, en cualquier punto del movimiento la energía total es contante, tenemos que:
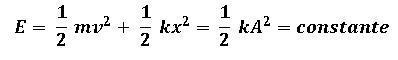

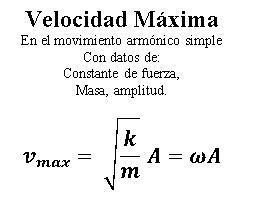
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM de Física Área 4-2023$90.00
Guía UNAM de Física Área 4-2023$90.00 -
 Guía UNAM de Física Área 3-2023$90.00
Guía UNAM de Física Área 3-2023$90.00 -
 Guía UNAM de Física Área 2-2023$90.00
Guía UNAM de Física Área 2-2023$90.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00 -
 Guía UNAM de Física Área 1-2023$90.00
Guía UNAM de Física Área 1-2023$90.00