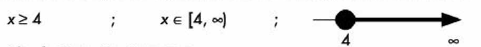DESIGUALDAD DE PRIMER GRADO EN UNA VARIABLE Y SUS PROPIEDADES
Las desigualdades de comparación son las relaciones de comparación entre expresiones algebraicas que tienen entre sus elementos una o más variables con exponente igual a 1.
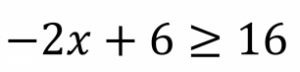
Las propiedades de las desigualdades de primer grado son:
1.- Propiedad transitiva:
Si a > b y b > c entonces a > c
2.- Propiedad aditiva y sustractiva
Si a < b entonces a + c < b + c
Si a < b entonces a – c < b – c
3.- Propiedad multiplicativa y divisoria
Si c es positivo:
a < b entonces a*c < b*c
a < b entonces a/c < b/c
Si c es negativo:
a < b entonces a*c > b*c
a < b entonces a/c > b/c
4.- Propiedad del opuesto
Si a < b entonces –a > -b
Si a > b entonces –a < -b
5.- Propiedad de reciproco
Si a y b con diferentes de cero y ambos tienen el mismo signo:
Si a < b entonces 1/a > 1/b
Si a > b entonces 1/a < 1/b
Si a y b tienen diferentes signos:
Si a < b entonces 1/a < 1/b
Si a > b entonces 1/a > 1 /b
Para resolver desigualdades, es decir, para encontrar los valores para los cuales es cierta la desigualdad se aplican los mismos criterios que para resolver igualdades (despeje de la variable).
La única diferencia es que los resultados son un conjunto de soluciones, este conjunto de soluciones se puede representar como un intervalo o como una gráfica.
La siguiente figura muestra las diferentes formas de representar las desigualdades:

Ejemplos de desigualdades de primer grado en una variable:
1.- Encontrar las soluciones para la desigualdad:
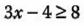
Despejando la variable obtenemos:
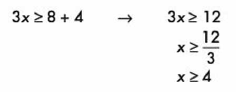
Y este resultado se puede representar de 3 formas: