RAZONES TRIGONOMÉTRICAS PARA UN ÁNGULO EN CUALQUIER CUADRANTE. FÓRMULAS DE REDUCCIÓN

SIGNOS DE LAS RAZONES TRIGONOMÉTRICAS SEGÚN EL CUADRANTE DEL ANGULO

---

Gracias al cuadro siguiente podemos saber el signo que tendrá la razón trigonométrica según el valor del ángulo:

Recuerda que:

                    1.- El primer cuadrante comprende de 0 a 90 grados

                    2.- El segundo cuadrante comprende de 90 180 grados

                    3.- El tercer cuadrante comprende de 180 a 270 grados

                    4.- El cuarto cuadrante comprende de 270 a 360 grados

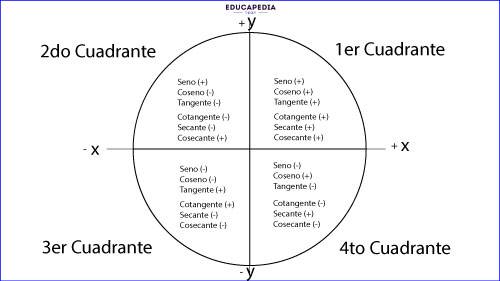
RECUERDA:

El seno del ángulo representa el valor de las ordenadas (y) en el plano cartesiano, por lo que en el cuadrante 1 y 2 (los cuadrantes superiores, los que tienen “y” positiva) el seno será positivo y en los cuadrantes 3 y 4 (los cuadrantes inferiores, los que tienen “y” negativa) el seno será negativo.

El coseno representa el valor de las abscisas (x) en el plano, por lo que, en el cuadrante 1 y 4 (los del lado derecho, los que tienen “x” positiva) el coseno será positivo, y en el cuadrante 2 y 3 (los del lado izquierdo, los que tienen “x” negativa) el coseno será negativo.

Y el signo de la tangente en el cuadrante será la multiplicación de signos del seno y el coseno en ese cuadrante.

FORMULAS DE REDUCCIÓN:

---

Las fórmulas de reducción son las fórmulas utilizadas en trigonometría para reducir los valores de los ángulos mayores a 90⁰ en ángulos entre 0 y 90 grados.

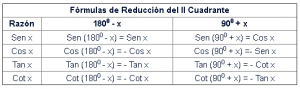
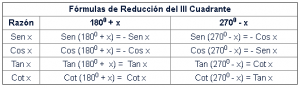
REGLAS PARA UTILIZAR LAS TABLAS DE REDUCCIÓN

---

1.- La razón trigonométrica de un ángulo mayor a 90 grados puede ser igual a 2 razones trigonométricas de un ángulo menor a 90 grados.

Por eso la tabla de reducción tienen dos columnas (no consideres la columna de la “razón”)

Por ejemplo:

Para reducir el seno 150⁰ podemos:

1era columna: Seno (180 -30) = Seno 30

2da columna: Seno (90 + 70) = Coseno 70

2.- Si utilizas la 1era columna la reducción será la misma función, pero respetando el signo del cuadrante original.

Por ejemplo:

Para reducir coseno 150⁰ tenemos:

1era columna: Coseno (180 -30) = -Coseno 30

3.- Si utilizas la 2era columna la reducción será la cofunción y también respetando el signo del cuadrante original.

Por ejemplo:

Para reducir coseno 150⁰ tenemos:

2da columna: Coseno (90 + 70) = -Seno 70

OTRO PROCEDIMIENTO PARA REDUCIR LOS ÁNGULOS MAYORES A 90 EN ANGULO MENORES A 90 GRADOS:

---

         1.- Recuerda los signos que tienen las relaciones trigonométricas dependiendo de su cuadrante

2.- Utiliza la formula siguiente para obtener el ángulo menor a 90 que es equivalente:

         Es decir:

Si tu ángulo es 150, entonces (1* 90 + 70)

           Si tu ángulo es 230, entonces (2*90 + 50)

3.- Si para obtener tu ángulo utilizaste:

                   N = par (2 y 4) entonces la respuesta es la misma relación trigonométrica con el signo correspondiente al cuadrante.

                   N = impar (1 y 3) entonces la respuesta en la cofunción trigonométrica con el signo correspondiente al cuadrante

Recuerda que las cofunciones son:

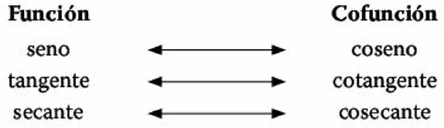
Ejemplos para obtener las razones trigonométricas de un ángulo en cualquier cuadrante:

1.- Calcula la relación trigonométrica equivalente a: cos 150.

         Primero obtenemos la relación de equivalencia:

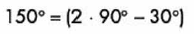
         Segundo, recordamos que el coseno es negativo en el 2dp cuadrante

         Y debido a que n = 2, es decir, par, nos da la misma función.

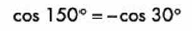
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.