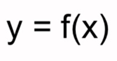FORMAS ORDINARIA Y GENERAL DE LA ECUACIÓN DE LA HIPÉRBOLA CON CENTRO EN EL ORIGEN Y EJE FOCAL SOBRE ALGUNO DE LOS EJES COORDINADOS

Las ecuaciones de la hipérbola con centro en el origen y su eje focal sobre algún eje coordenado son:

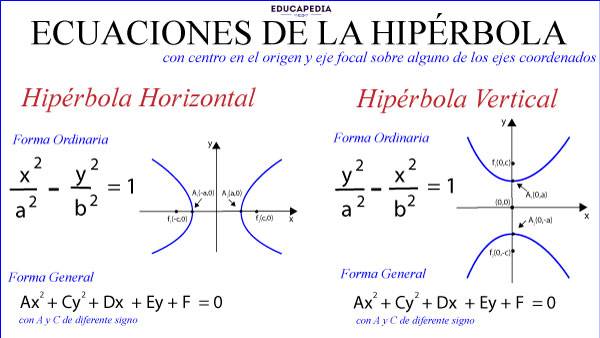
FORMA ORDINARIA DE LA ECUACIÓN DE LA HIPÉRBOLA HORIZONTAL CON CENTRO EN EL ORIGEN Y EJE FOCAL COINCIDE CON EJE X

---

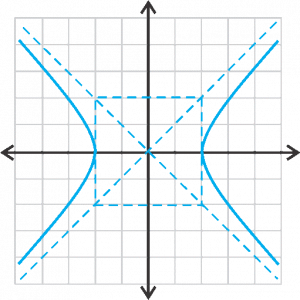
PROPIEDADES DE LA GRAFICA DE LA HIPÉRBOLA HORIZONTAL CON CENTRO EN EL ORIGEN

Con vértices: V1(a, 0) y V2(-a, 0)

Focos: F1(c,0) y F2(-c,0)

Extremos del eje conjugado:

B1(0, b) y B2(0, -b)

Asíntotas: y = +-(b/a)(x)

FORMA ORDINARIA DE LA ECUACIÓN DE LA HIPÉRBOLA VERTICAL CON CENTRO EN EL ORIGEN

PROPIEDADES DE LA GRAFICA DE LA HIPÉRBOLA VERTICAL CON CENTRO EN EL ORIGEN

Con vértices: V1(0,a) y V2(0,-a)

Focos: F1(0,c) y F2(0,-c)

Extremos del eje conjugado:

B1(b,0) y B2(-b,0)

Asíntotas: y = +-(a/b)(x)

FORMA GENERAL DE LA ECUACIÓN DE LA HIPÉRBOLA CON CENTRO EN EL ORIGEN

---

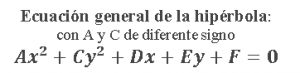
DETALLES DE LA GRAFICA DE LA HIPÉRBOLA CON CENTRO EN EL ORIGEN Y SU ECUACIÓN ORDINARIA

---

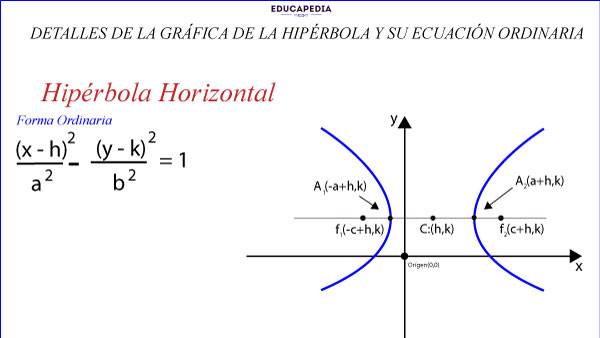
Nota Importante:

Fíjate que en la grafica de la hipérbola no se puede determinar el parámetro “b” y en su ecuación ordinaria no te da el valor de “c” para.

Esto se resuelve con la relación de sus parámetros que vimos en el capítulo anterior.

Ejemplos de la ecuación de la hipérbola con centro en el origen:

1.-Determina las coordenadas de los vértices de la hipérbola:

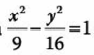
         Primero determinados que orientación tiene esta hipérbola, como tiene la forma:

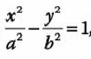
         Tenemos que es horizontal con centro en el origen.

         Así que obtenemos los valores de los parámetros a y b:

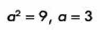
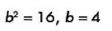
         Con esto determinamos los vértices y tenemos que:

         V1(3, 0) V2(-3, 0)

ORIGEN DE LA ECUACIÓN DE LA HIPÉRBOLA

Para construir la ecuación de la hipérbola partimos de la definición matemática de la hipérbola y tenemos que:

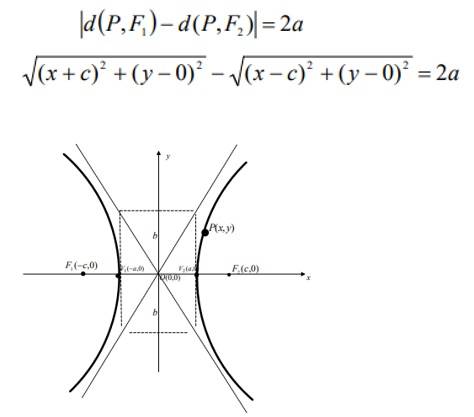
Despejando un radical, elevando al cuadrado y reduciendo términos semejantes:

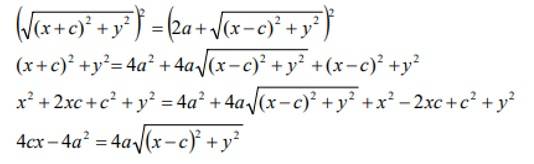
Dividiendo entre 4, elevando al cuadrado y reduciendo términos semejantes:

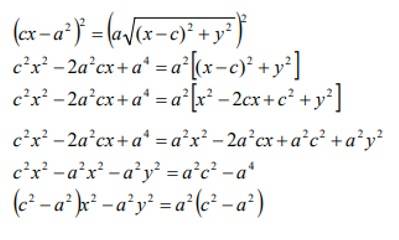
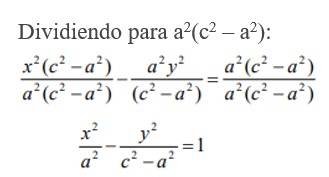
Utilizando la relación de sus factores b² = c² – a² tenemos:

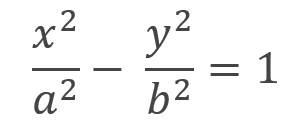
De la misma forma, la ecuación de la hipérbola con centro en (h, k) es:

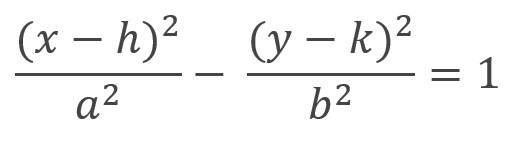
Donde:

b representa el semieje conjugado

a representa el semieje transverso

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.