RELACIÓN ENTRE LOS PARÁMETROS DE LA HIPÉRBOLA A, B Y C

DEFINICIÓN DE LOS PARÁMETROS DE LA HIPÉRBOLA

---

a = Es la distancia del centro de la hipérbola a uno de sus vértices

b = Es la distancia del centro de la elipse a un punto sobre su eje conjugado que tiene como distancia a un vértice igual a la distancia entre el centro y un foco.

c = Es la distancia de un punto sobre el eje conjugado a un foco.

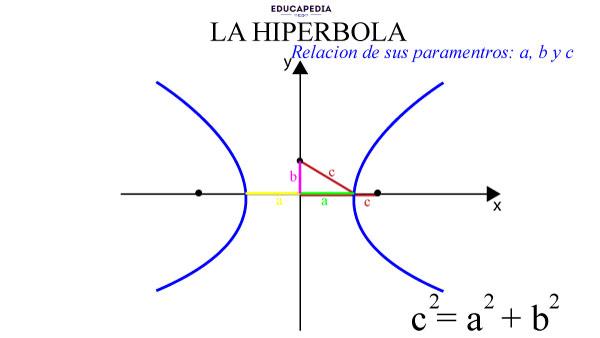
Si trazamos un triángulo rectángulo en la hipérbola y utilizamos el Teorema de Pitágoras, podemos observar que:

c² = a² + b²

Es decir; el cuadrado del semieje focal es igual a la suma de los cuadrados del semieje transverso más el semieje conjugado.

EXCENTRICIDAD DE LA HIPÉRBOLA:

---

Definimos la excentricidad como:

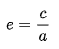
Donde:

         c = semieje focal = ½ de la distancia focal

         a = semieje mayor = ½ de la distancia de eje mayor

Donde:

          c = semieje focal = ½ de la distancia focal

          a = semieje mayor = ½ de la distancia de eje mayor

¡IMPORTANTE!

En la elipse, a es la hipotenusa del triangulo para formar la relación: a² = b² + c². En la hipérbola c es la hipotenusa para formar la relación de sus parámetros: c² = a² + b².

Te puede ayudar si recuerdas que la hipotenusa se forma con el parámetro mas largo de su respectiva cónica.

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.