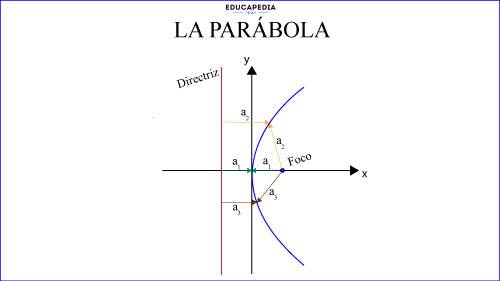
PARÁBOLA COMO LUGAR GEOMÉTRICO

Definición de parábola como lugar geométrico

La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.

Es decir, que la distancia entre cualquier punto de la parábola hacia el foco que esta “dentro” de la parábola y la distancia hacia la directriz que esta “afuera” de ella, es la misma.

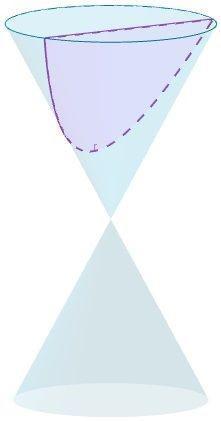
También, la parábola, se define como la sección cónica que resulta de cortar un cono con un plano inclinado.

Este lugar geométrico también se obtiene de una ecuación de segundo grado, de la forma:

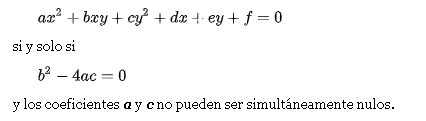
Nota: El aspecto matemático de la parábola nos enfocaremos en los siguientes capítulos.

PROPIEDADES FÍSICAS DE LA PARÁBOLA:

---

Una de las propiedades de la parábola se da cuando un conjunto de rayos paralelos al eje de simetría que incide en una superficie reflectora con forma de parábola, se reflejan en dirección al foco, es decir, se concentran en un punto.

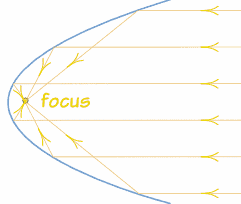
Por eso, son utilizadas para construir antenas, radares, espejos, etc. Porque en el “foco”, se concentran, se “enfocan” todos los rayos.

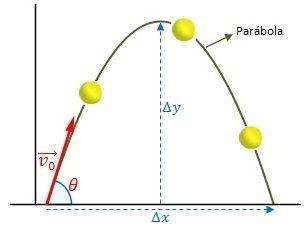
En física, los cuerpos que se lanzan hacia arriba con cierta inclinación, describen movimientos parabólicos.

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.