INTEGRAL DEFINIDA Y SU NOTACIÓN

Definición de integral definida

La integral definida de una función f(x) es igual a la diferencia de los valores que toma su primitiva en los extremos superior e inferior de un intervalo.

Su notación es:

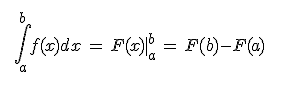
Siendo F(x) una primitiva de f(x)

PROPIEDADES DE LA INTEGRAL DEFINIDA:

---

Ver ejemplo de obtención de una integral definida en la sección de abajo.

INTERPRETACIÓN GEOMÉTRICA DE LA INTEGRAL DEFINIDA

---

Bajo ciertas condiciones, la integral definida de F en el intervalo [a, b] es igual al área bajo la curva F(x) y el eje de las abscisas entre “a” y “b”.

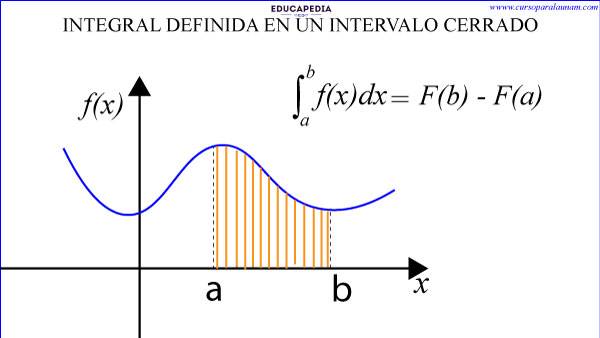
Lo cual se expresa como:

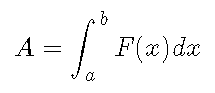
ÁREA BAJO DOS CURVAS

La integral definida en un intervalo cerrado también se puede utilizar para calcular el área entre dos curvas:

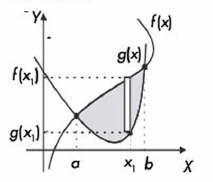
Sean las curvas f(x) y g(x) definidas en el intervalo [a, b], el área comprendida entre ellas está dada por la fórmula:

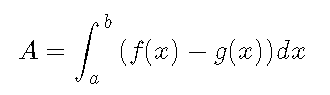
Donde a y b son las coordenadas del eje “x” donde se cortan las curvas.

Ejemplos de integral definida:

1.- Calcula la siguiente integral:

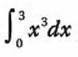
         Aplicando nuestra formula tenemos:

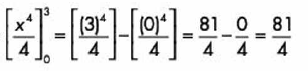
2.- Calcula el área formada entre la siguiente función, el eje “x” y las rectas x = 0 y, x = 4:

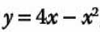
         Primero expresamos el problema en términos de la integral definida:

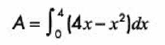
         Al resolver nuestra integral definida obtenemos:

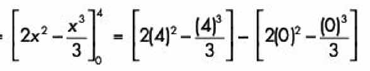
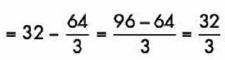
         Y las unidades las consideramos como unidades cuadradas.

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.