CONTINUIDAD EN UN PUNTO Y EN UN INTERVALO
Intuitivamente la continuidad de una función, es que su grafica se pueda dibujar sin alzar la pluma del plano.
Es decir, para los valores “x” que nosotros determinemos, debe haber valores f(x).
CONTINUIDAD EN UN PUNTO
En términos de límites podemos decir que una función es continua en un punto x0 si:
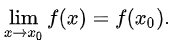
Aunque también podemos decir que una función es continua en un punto x0 si está definida en ese punto f(x0)
Es decir: podemos decir que una función es continua de 3 formas:
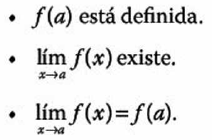
CONTINUIDAD EN UN INTERVALO
Una función f(x) es continua en un intervalo abierto (a, b), si es continua en todo punto del intervalo.
Una función f(x) es continua en un intervalo cerrado [a. b] si es continua en (a, b) y:
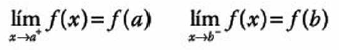
Ejemplos de continuidad en un punto y en un intervalo:
1.- Determina cuál de los siguientes valores, la función es continua:
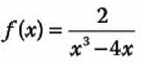

Sustituyendo para cada valor tenemos:
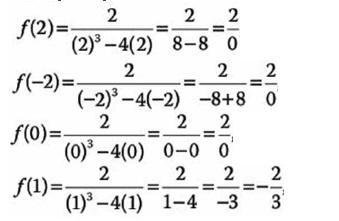
Determinamos que solamente para -2/3 la funciones está definida, por lo tanto, en ese punto es continua.
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00







