FORMAS ORDINARIA Y GENERAL DE LA ECUACIÓN DE LA PARÁBOLA CUANDO EL VÉRTICE ESTÁ EN EL ORIGEN Y EL EJE FOCAL COINCIDE CON ALGUNO DE LOS EJES COORDENADOS

Las formas ordinaria y general de la ecuación de la parábola con vértice en el origen y eje focal coinciden con alguno de los ejes coordenados son:

FORMA ORDINARIA DE LA ECUACIÓN DE LA PARÁBOLA CON VÉRTICE EN EL ORIGEN

---

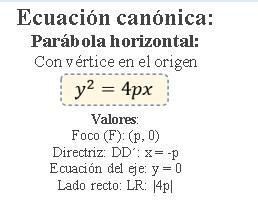
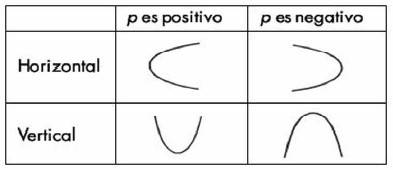
Concavidad:

         Si p > 0 la parábola es cóncava hacia la derecha (abre hacia la derecha)

         Si p < 0 la parábola es cóncava hacia la izquierda (abre a la izquierda)

Concavidad:

         Si p > 0 la parábola es cóncava hacia arriba (abre hacia arriba)

         Si p < 0 la parábola es cóncava hacia abajo (abre hacia abajo)

DETALLES GRAFICOS DE LA ECUACION DE LA PARABOLA EN SU FORMA ORDINARIA

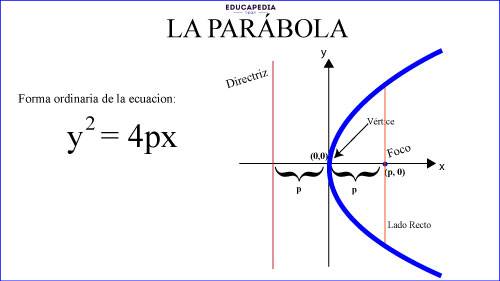
LOS 4 TIPOS DE PARABOLA CON VERTICE EN EL ORIGEN Y EJE FOCAL COINCIDE CON ALGUN EJE COORDENADO

Resumiendo:

El sentido de apertura de la parábola tenemos que:

ECUACIÓN GENERAL DE LA PARÁBOLA CON VÉRTICE EN EL ORIGEN

---

ORIGEN DE LA ECUACIÓN DE LA PARÁBOLA

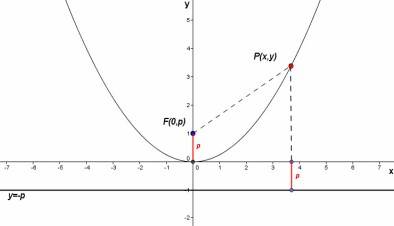
Debido a la definición de parábola, la distancia del foco (F) al punto (P) es igual a la distancia de este mismo punto a la directriz. Lo cual expresamos en notación matemática como:

La distancia del foco (F) al punto (P):

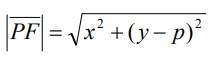
La distancia del punto (P) a la directriz:

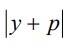
Por lo tanto:

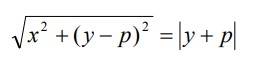
Si elevamos ambos miembros al cuadrado, desarrollamos binomios y agrupamos términos, tenemos que:

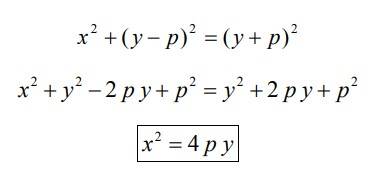
Este mismo procedimiento se puede aplicar para obtener la ecuación de la parábola vertical hacia abajo y horizontal hacia la derecha e izquierda.

ORIGEN DE LA ECUACIÓN GENERAL DE LA PARÁBOLA

---

La ecuación general de la parábola se obtiene cuando se desarrolla la ecuación ordinaria con vértice en cualquier punto del plano.

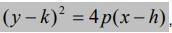
Se desarrolla el binomio, se agrupan términos semejantes y obtenemos una ecuación de la forma:

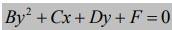
Como la parábola puede ser vertical u horizontal, escribimos la ecuación general como:

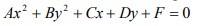
Y decimos que es de una parábola, siempre y cuando A o B sean iguales a 0. Pero no ambos simultáneamente.

Ejemplos de la ecuación de la parábola con vértice en el origen

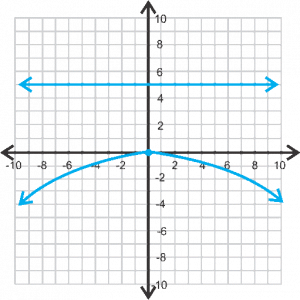
1.- Determina el foco, la directriz y grafica la parábola de la siguiente ecuación:

         y² = -12 x

         Primero calculamos “p”:

         -12 = 4p

         p = -3

         Debido a que “y” es la variable que esta al cuadrado, tenemos que la parábola es HORIZONTAL, y debido a que “p” es negativo sabemos que la parábola se abrirá hacia la izquierda

         Por lo tanto:

         Foco: (-3, 0)

         Directriz: x = 3

         Por ultimo, traza la parábola en el plano cartesiano.

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.