FUNCIONES EXPONENCIALES Y LOGARÍTMICAS
Las funciones exponenciales y logarítmicas son las funciones que se basan en las operaciones de potenciación (ax) y su operación inversa que son los logaritmos (log x).
LA FUNCIÓN EXPONENCIAL
La función exponencial es el conjunto de valores donde a cada valor que le vamos dando a “x”, el valor de “y” será igual a la constante elevada a la “x”.

La frase: “crece exponencialmente”, nos referimos a que conforme aumentamos “x”, la variable dependiente “y” va obteniendo valores más grandes cada vez.
Ejemplo:
En la función y = 2x, le vamos dando valores a “x”: 1, 2, 3, 4…es decir, va creciendo de uno en uno; pero cuando obtenemos los valores de “y” tenemos: 2, 4, 8, 16…es decir, su crecimiento se va duplicando en cada valor.
TIPOS DE FUNCIÓN EXPONENCIAL
La función exponencial presenta dos casos especiales:
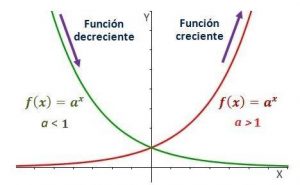
1.- Cuando a > 1
2.- Cuando 0 < a < 1
Cuando a > 1
1.- La grafica de la función será creciente en todo su dominio
Cuando a < 1
1.- La grafica de la función será decreciente en todo su dominio
DOMINIO: (-∞, ∞)
CODOMINIO: (0, ∞)
¡OJO!
En todos los casos los valores de “y” serán positivos, es decir, su codominio será (0, ∞).
Ejemplos:
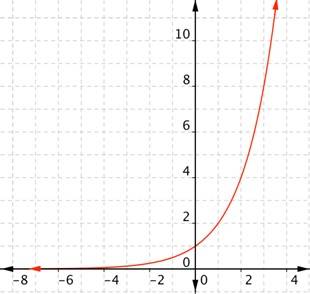
1.- En el crecimiento de las bacterias, algunas colonias de estas se duplican cada hora. Si comienzan con 1 bacteria y se duplica en cada hora, se tendrá 2x bacterias después de “x horas”. Esto se expresa como:
F(x) = 2x y tiene como desarrollo:

Y su gráfica es la siguiente:
Recuerda:
En una función exponencial, la variable independiente forma parte del exponente.
CASO ESPECIAL DE FUNCIÓN EXPONENCIAL
Existe un caso especial de función exponencial cuando la base es igual a “e”.
En este caso tenemos que:
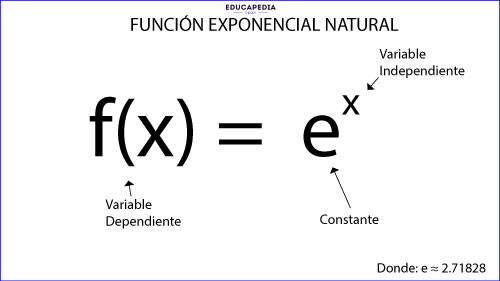
Recuerda:
“e” es una constante y nace de la siguiente definición:

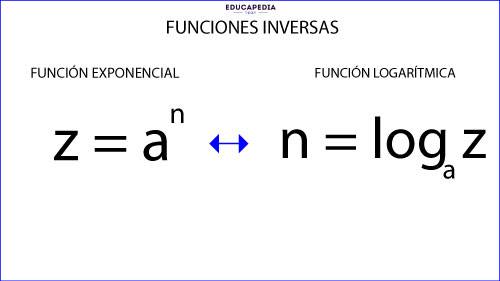
LA FUNCIÓN LOGARÍTMICA:
La función logarítmica es el conjunto de valores donde a cada valor que le vamos dando a “x”, el valor de “y” es igual a un número, el cual cumple que ay = x.
Es decir:
“y” es el exponente que buscamos para elevar la base y nos dé “x”.
La función logarítmica es de la forma:

“La función logarítmica es la función inversa a la función exponencial”
Ejemplo:
El logaritmo decimal (base 10) de 100 es 2, porque 102 = 100
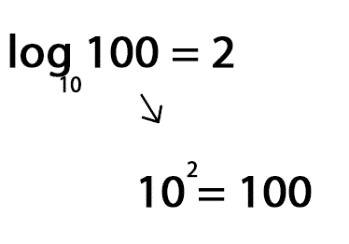
Cuando decimos que algo “crece o decrece logarítmicamente”, damos a entender que su crecimiento o decrecimiento cada vez se hace más pequeño, aunque los valores de “x” sigan aumentando de la misma manera.
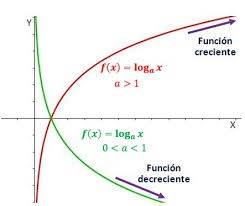
TIPOS DE FUNCIONES LOGARÍTMICAS
De la misma forma que las funciones exponenciales, también en las funciones logarítmicas se presentan dos tipos de funciones:
1.- Cuando “a” > 1
2.- Cuando 0 < a < 1
Cuando a > 1
1.- La grafica de la función será también será creciente en todo su dominio de la misma forma que la función exponencial.
Cuando a < 1
1.- La grafica de la función será también será decreciente en todo su dominio de la misma forma que la función exponencial.
DIFERENCIA DE LA FUNCIÓN LOGARÍTMICA CON LA FUNCIÓN EXPONENCIAL
La diferencia con la función exponencial es que los “x” (el dominio) de la función exponencial serán solo el segmento (0, ∞), y los valores que “y” podrá adquirir, ahora pueden ser de (-∞, ∞).
Es decir, exactamente lo contrario que la función exponencial.
FUNCIONES LOGARÍTMICAS ESPECIALES
Dentro de las funciones logarítmicas existen dos casos especiales:
1.- Los logaritmos comunes o de base 10, abreviados como (Log x)
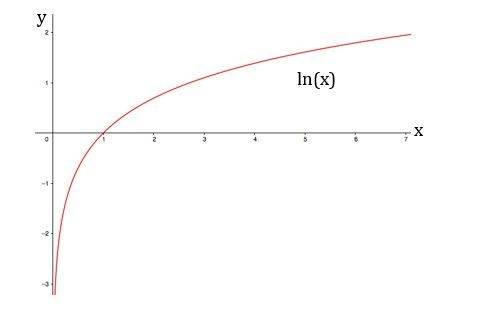
2.- Los logaritmo naturales o neperianos de base “e”, abreviados como (In x)

Gráfica del logaritmo natural:
PROPIEDADES DE LOS LOGARITMOS:

EJEMPLOS DE LAS PROPIEDADES DE LOS LOGARITMOS:

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00







