MÉTODOS DE INTEGRACIÓN
INTEGRACIÓN POR PARTES
La integración por partes es el método más usado para resolver la integral de una función y consiste en descomponer la integral en un producto de dos términos (u y dv) y aplicar la formula siguiente:
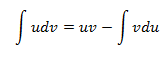
Generalmente se utiliza cuando el integrando está formado por un producto, o una división (que se puede tratar como un producto).
PROCEDIMIENTO DE INTEGRACIÓN POR PARTES:
1.-El integrando debe ser producto de 2 factores
2.-Uno de los factores será “u” y el otro será “dv”.
3.-Se calcula “du” derivando “u” y se calcula “v” integrando “dv”.
4.-Por último, se aplica la formula
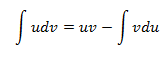
Sugerencia importante:
Escoge “u” como el factor mas complicado de integrar para que de esta manera no lo tengas que integrar sino solamente derivar.
Escoge “dv” al factor más fácil de integrar.
Generalmente escogemos a los factores del integrando que tienen inversas y logaritmos como “u”, y a los factores que tienen exponenciales, fracciones y funciones trigonométricas como “dv”.
Ver ejemplo de integración por partes mas abajo.
MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE
Este método se basa en realizar una sustitución de variables adecuado que permita convertir el integrando en una integral más sencilla o en una integral inmediata.
PROCEDIMIENTO PARA INTEGRAR POR SUSTITUCIÓN DE VARIABLE.
1.- Se selecciona la operación más simple del integrando que este complicando la integración.
2.- Se sustituye esta operación simple con respecto a la variable “x” por una función con diferente variable. Es decir; x = g(t)
3.- Se sustituye esta nueva función con diferente variable en el integrando
4.- Se resuelve la integral en términos de la nueva variable
5.- El resultado se reemplaza nuevamente por la variable original.
Sugerencia:
Regularmente se utilizan las integrales inmediatas como integrales de una función: es decir, f(x) = v
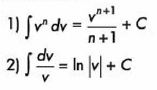
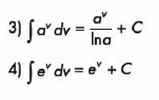
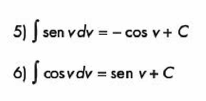
EJMEMPLOS DE INTEGRACIÓN POR PARTES:
1.- Determina la siguiente integral:
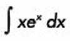
Elegimos u y dv, y obtenemos du y v:
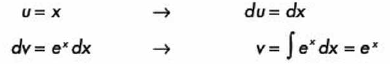
Utilizando nuestra formula:
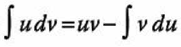
Tenemos que:
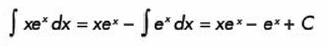
EJEMPLOS DE INTEGRACIÓN POR CAMBIO DE VARIABLE:
1.- Determina la siguiente integral:
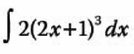
Utilizamos la fórmula:
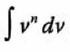
Hacemos el cambio de variable:
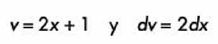
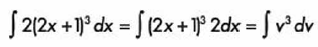
Resolvemos la integral y volvemos a sustituir las variables:
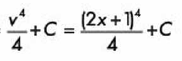
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00