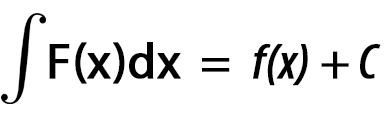BINOMIO DE NEWTON (A+B) N
Definición del Binomio de Newton
El Binomio de Newton (también conocido como el Teorema del Binomio) es una formula general que nos ayuda a el desarrollo de un binomio a la potencia n-ésima.
Es decir, con la fórmula del Binomio de Newton se pueden desarrollar todos los términos de un binomio a la potencia que uno desee.
FORMULA DEL BINOMIO DE NEWTON:

El desarrollo del Binomio de Newton es el siguiente:
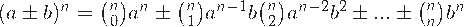
MÉTODO PARA DESARROLLAR EL BINOMIO DE NEWTON:
1.- NUMERO DE TÉRMINOS DEL DESARROLLO
El número de términos que tendrá el desarrollo serán igual a n + 1:
Si el binomio esta elevado a la potencia 4, entonces el desarrollo tendrá 5 términos
Si esta elevado a la 5, tendrá 6 términos, y así sucesivamente,
2.-COEFICIENTES DE LOS TÉRMINOS
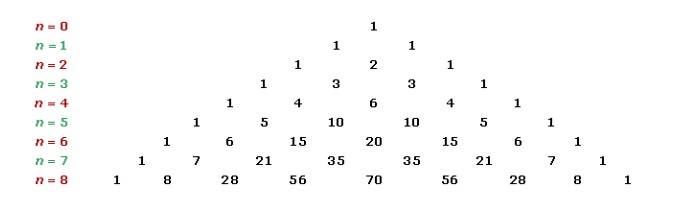
Para potencias pequeñas puedas utilizar el Triángulo de Pascal para obtener los coeficientes de cada termino.
O utilizar la fórmula: Donde k es el número del término el cual se busca el coeficiente y n es la potencia que esta elevada el binomio.

3.- EXPONENTES DE LAS VARIABLES
Los exponentes de “x” van disminuyendo de uno en uno, de “n” hasta cero.
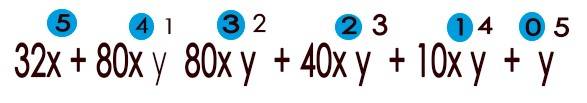
Los exponentes de “y” van aumentando de uno en uno de cero hasta “n”, de tal manera que la suma de los exponentes de cada termino es igual a “n”.
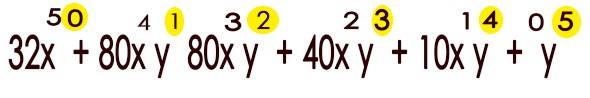
OJO:
La suma de los exponentes de las variables de cualquier termino del desarrollo es igual a “n”, la potencia del binomio.

O utilizar la formula:

5.- SIGNOS DE LOS TÉRMINOS
Si los dos elementos del binomio son positivos (x + y)n; todos los términos del desarrollo serán positivos
Si el segundo elemento del binomio es negativo, se alternan los signos positivos y negativos en el desarrollo, empezando por positivo.
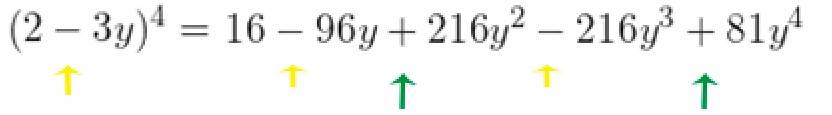
O se puede aplicar la siguiente formula a binomios de la forma (x – y)n

RECOMENDACIÓN:
Para calcular el signo del término k-esimo de término del desarrollo del binomio de Newton:
1.- Primero calcula los exponentes de las variables del término.
2.- Sustituye la variable por -1 o +1 según sean negativo o positivo la variable del binomio
3.- Realiza la potencia indicada en cada variable.
4.- Multiplica el resultado y ese será el signo del término correspondiente.

Ejemplos del Binomio del Newton:
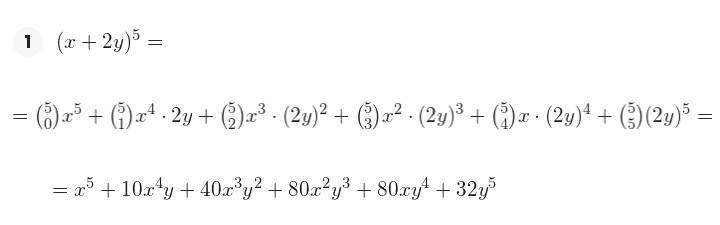

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00