DEFINICIÓN FORMAL DE LIMITE
DEFINICIÓN FORMAL DE LIMITE
El límite de una función f(x), cuando x tiende a x0 es igual a L, “si y solo si para todo número real positivo Ɛ, existe otro real positivo δ, tal que, para todos los valores de x distintos de x0 que cumplen la condición |x – x0| < δ se cumple |f(x) – L| < Ɛ
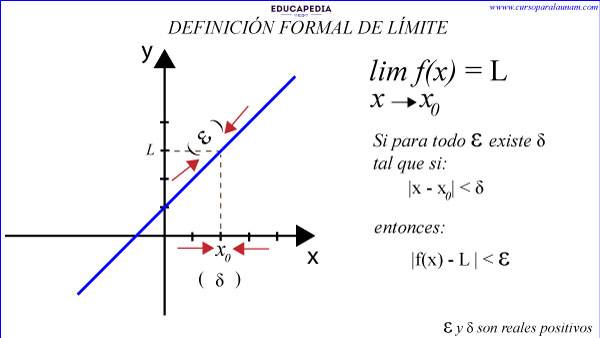
En términos muy simples y generales, quiere decir, que existe un límite en una función, si existen valores “x” tan cercanos a x0 que tengan sus imágenes f(x) o valores “y” tan cercanos al límite (L).
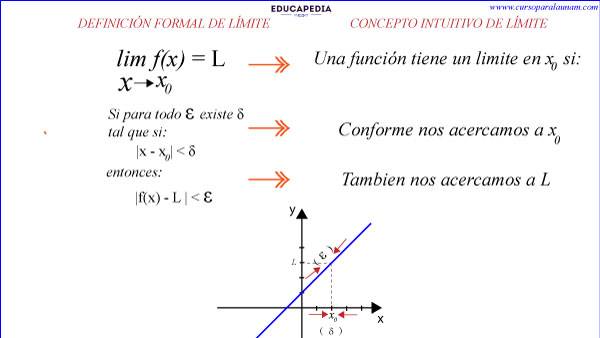
Es decir, que como nos vayamos acercando a x0, también nos tenemos que ir acercando a L, pues si no nos acercarnos a L, conforme nos acercarnos a x0, entonces no existiría el límite en esa función.
Como en la definición se mencionó, valores absolutos, (|x – x0| < δ se cumple |f(x) – L| < Ɛ) esto significa que los valores existen tan cerca del lado izquierdo como del lado derecho.
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00







