FORMAS DE LA ECUACIÓN DE LA RECTA Y SU GRAFICA
Con la ecuación de la pendiente de la recta podemos obtener todas las formas de la ecuación.

Si consideramos a uno de los puntos (x2, y2) como (x, y) y despejamos, podemos obtener las diferentes formas de la ecuación:
1.- ECUACIÓN GENERAL DE LA RECTA:
Ax + By + C = 0
Donde A, B y C son constantes
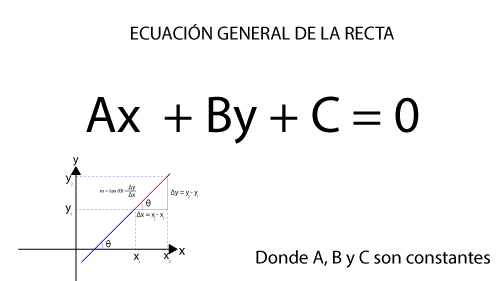
Ejemplo de la ecuación general de la recta:
1.- Determina el valor de la pendiente de la recta: 5x -4y -8 = 0
Como ya vimos, podemos cambiar la forma de la ecuación, así que a la ecuación anterior despejamos “y” para obtener la forma de la ecuación con pendiente m y ordenada en el origen b:
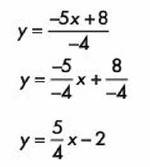
Con lo que podemos observar que m= 5/4
2.- ECUACIÓN DE LA RECTA CON PENDIENTE “m” Y ORDENADA EN EL ORIGEN (b):
y = mx + b
Donde m = pendiente y
b = ordenada en el origen
Nota: “b” se le llama ordenada en el origen porque cuando “x = 0”, “y = b”, es decir, la recta pasa por el punto (0, b)
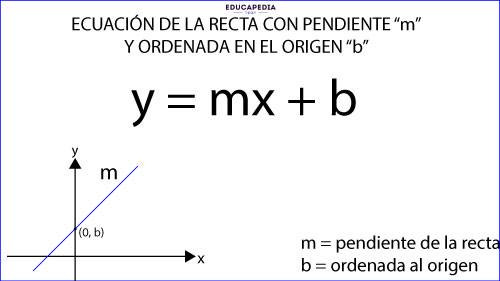
Ejemplos de la ecuación de la recta con pendiente “m” y ordenada en el origen “b”:
3.- Determina la ecuación de la recta que intercepta al eje Y en -6 y tiene una pendiente de -7:
Primero determinamos los valores que vamos a sustituir:
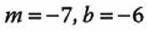
Sustituimos en la ecuación de la recta con pendiente m y ordenada en el origen “b”:
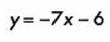
Y también la podemos expresar como forma general:
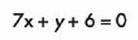
3.- ECUACIÓN DE LA RECTA PUNTO – PENDIENTE:
y – y1 = m (x – x1)
Donde m = pendiente y
(x1, y1) es el punto
por donde pasa la recta.

Ejemplos de la ecuación de la recta punto-pendiente:
1.- Forma la ecuación de la recta que pasa por el punto (4, -6) y con pendiente = 2:
Primero utilizamos la ecuación punto pendiente de la recta porque esos son los valores que tenemos:
Segunda, determinamos los valores que vamos a sustituir:
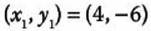
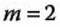
Tercera, sustituimos y obtenemos:
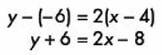
4.- ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS:
Donde las coordenadas de los puntos son:
(x1, y1) y (x2, y2)

Ejemplos de la ecuación de la recta que pasa por dos puntos:

5.- FORMA SIMÉTRICA DE LA ECUACIÓN DE LA RECTA:
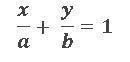
Donde “a” es el valor del eje “x” por donde pasa la recta y
“b” el valor del eje “y” por donde pasa la recta
Ejemplos de la forma simétrica de la ecuación de la recta:

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00