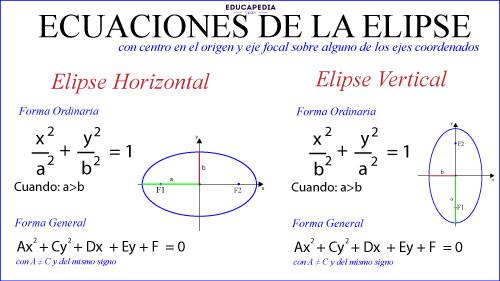
FORMAS ORDINARIA Y GENERAL DE LA ECUACIÓN DE LA ELIPSE CON CENTRO EN EL ORIGEN Y EJE FOCAL SOBRE ALGUNO DE LOS EJES COORDENADOS

Las ecuaciones de la elipse con centro en el origen y su eje focal sobre alguno de los ejes coordenados en su forma ordinaria y general son:

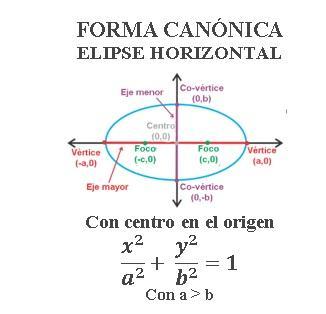
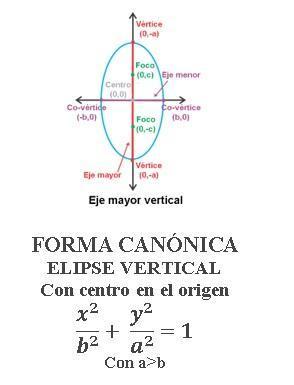
ECUACIÓN CANÓNICA DE LA ELIPSE CON CENTRO EN EL ORIGEN

---

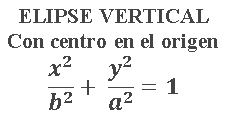
ECUACIÓN GENERAL DE LA ELIPSE CON CENTRO EN EL ORIGEN:

---

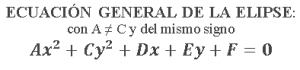
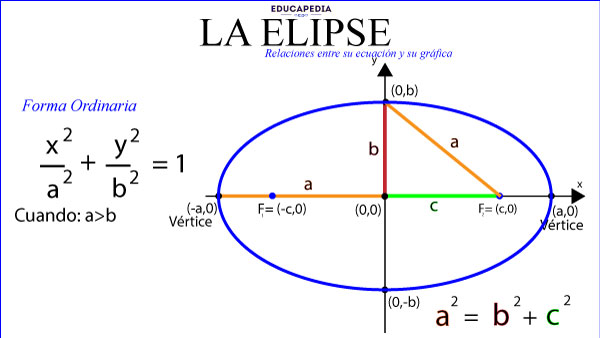
DETALLES DE LA GRAFICA Y LA ECUACIÓN DE LA ELIPSE CON CENTRO EN EL ORIGEN Y EJE FOCAL SOBRE EL EJE X

---

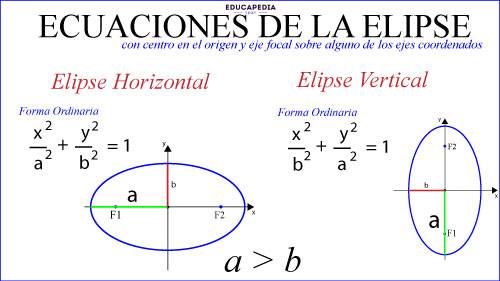
IDENTIFICAR SI UNA ELIPSE ES HORIZONTAL O VERTICAL:

---

Para identificar si la elipse es horizontal o vertical, solo hay que fijarse sobre que variable está el denominador mayor.

Si el denominador de “x” es mayor, la elipse es horizontal. Porque ese eje es el más largo (a).

Si el denominador de “y” es mayor, la elipse es vertical, porque ahora ese eje sería el más largo (a).

¡Nota!

a siempre es mayor que b. Si son iguales, estamos frente a una circunferencia.

Ejemplos de la ecuación de la elipse con centro en el origen:

1.- Determina los vértices, los focos y la gráfica de:

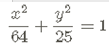
Solución:

         Primero determinamos si la elipse es horizontal o vertical:

         Como 64 > 25 el eje más largo esta sobre el eje “x” por lo tanto es horizontal.

         Después tenemos que a² = 64 y b² = 25

         Por lo que tenemos que a = 8 y b = 5

Y con esto determinamos los vértices que son:

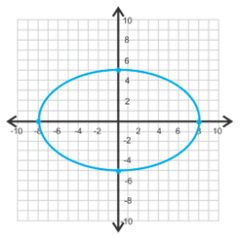
         V₁ (8, 0) y V₂(-8, 0)

Para encontrar los focos usamos la relación de sus parámetros:

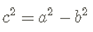
         Sustituimos y resolvemos:

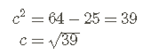
         Por lo que sus focos son:

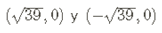
Y su grafica es:

El origen de la ecuación de la elipse, no forma parte del temario para el examen, sin embargo, creemos que es importante tener una idea de donde se obtiene, ya que esto facilita la comprensión de sus ecuaciones.

Además, si quieres practicar su algebra, desarrolla la ecuación por ti mismo.

ORIGEN DE LA ECUACIÓN DE LA ELIPSE

---

De la definición de elipse tenemos que:

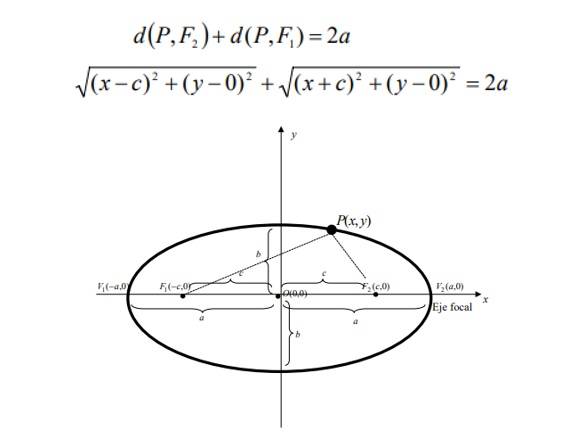
Despejando el radical, elevando al cuadrado y reduciendo términos semejantes obtenemos:

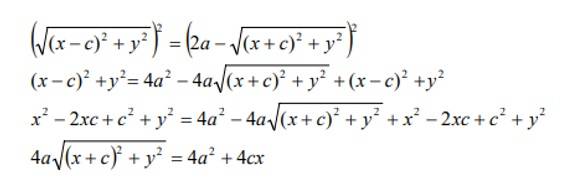
Dividiendo entre 4, elevando al cuadrado y reduciendo términos semejantes:

Utilizando la relación de sus factores b² = a² – c² tenemos:

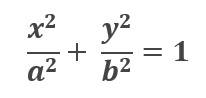
Y de la misma forma, la ecuación de la elipse con centro en (h, k) es:

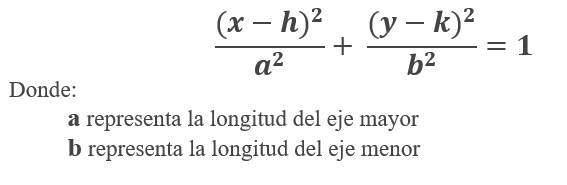
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.