RAÍCES Y POTENCIAS CON EXPONENTE RACIONAL CON NÚMEROS REALES
Conceptos básicos de raíces y potencias
Potencia: Es la representación del producto de una base por sí mismo, un cierto número de veces (exponente).
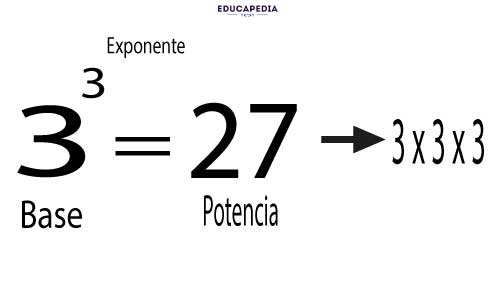
Raíces: Es la operación que permite encontrar un número que, multiplicado por sí mismo, tantas veces como lo indica el índice, da como resultado el radicando.
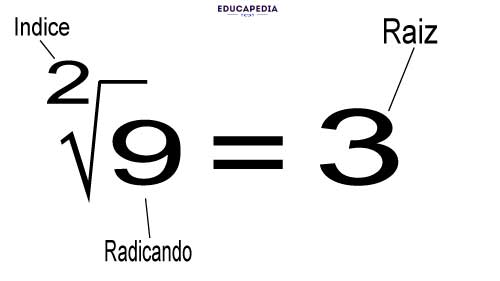
Ejemplos de potencias con números reales:

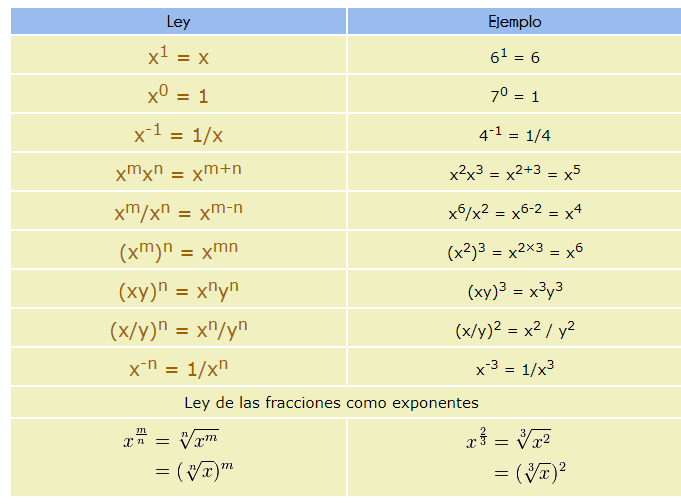
LEYES DE LOS EXPONENTES Y DE LOS RADICALES

Apréndete bien estas equivalencias porque no hay otra forma de deducirlas.
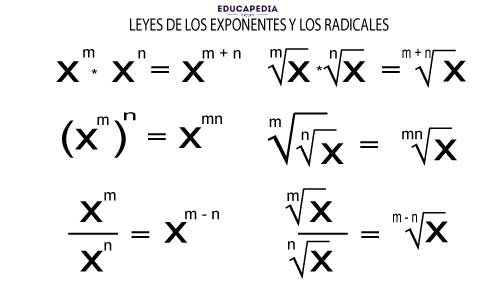
Fíjate que las leyes de los radicales (las del lado derecho) son idénticas a la de los exponentes, recuerda que un radical se puede expresar como un exponente.
Otro punto, es que todas las leyes anteriores se aplican cuando tienen la misma base (x).
Ejemplos de aplicación de las leyes de los exponentes:
POTENCIAS CON EXPONENTE FRACCIONARIO

Ejemplos de operaciones con exponentes y raices:

PROPIEDADES DE LOS EXPONENTES Y LOS RADICALES

Fíjate que estas propiedades a diferencia de las leyes de los exponentes y radicales, se aplican cuando la base es diferente.
SUMA Y RESTA DE EXPONENTES Y RADICALES

OJO:
Para sumar y restar radicales deben tener el mismo índice y el mismo radicando:
Observación:
Las leyes y las propiedades de los radicales son exactamente iguales a la de los exponentes, simplemente exprese los radicales en exponentes.
Ejemplos de suma y resta con radicales:
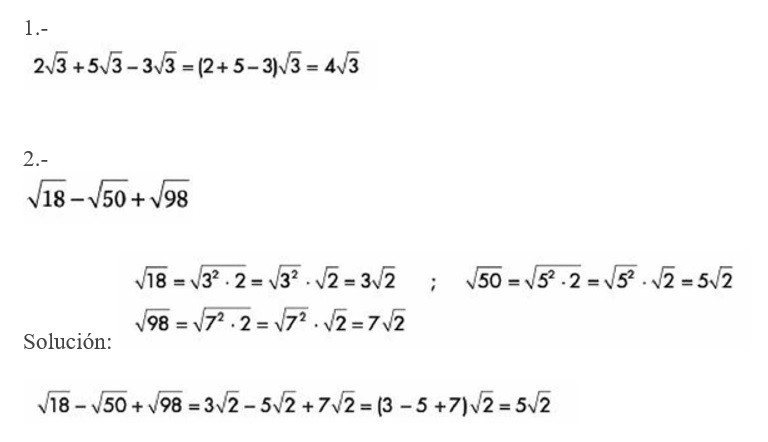
SIMPLIFICACIÓN DE RADICALES
La simplificación de radicales es el uso de operaciones aritméticas o de orden de términos matemáticos para convertir un radical en su expresión más simple.
Se utiliza para obtener términos semejantes y así poder hacer operaciones con otros elementos.
El procedimiento de la simplificación de los radicales es ir obteniendo términos semejantes ocupando las leyes y las propiedades de los exponentes y los radicales hasta obtener el termino mas simple o el termino deseado.
Ejemplos:
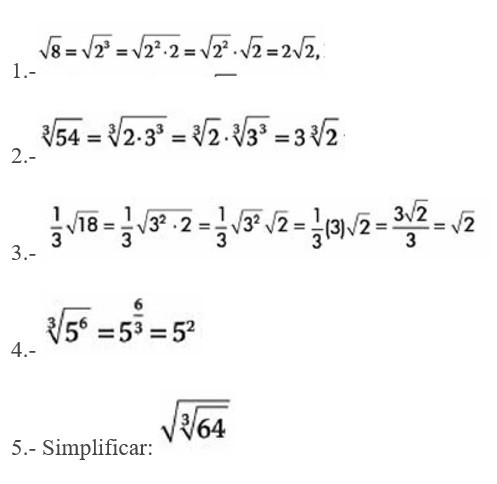
RACIONALIZACIÓN
Racionalizar es el conjunto de operaciones mediante el cual se convierte una fracción que contenga una raíz en el denominador, en otra fracción equivalente, cuyo denominador NO tenga un radical.
RACIONALIZACIÓN DE UN DENOMINADOR MONOMIO

Recuérdese que, si a una fracción se le multiplica o divide el denominador y el numerador por una misma cantidad, da como resultado una fracción equivalente, es decir, con el mismo valor.
Ejemplos de racionalización:

RACIONALIZACIÓN DE UN DENOMINADOR BINOMIO
Para racionalizar este tipo de fracción se multiplica por su conjugado.
El conjugado de un binomio (a + b) es el binomio (a – b).
El producto de dos binomios conjugados da como resultado una diferencia de cuadrado.
(a + b) (a – b) = a2 + b2
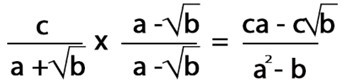
Ejemplos de racionalización de un denominador binomio:

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00