RELACIÓN ENTRE LOS PARÁMETROS A, B Y C DE LA ELIPSE

DEFINICIÓN DE LOS PARÁMETROS DE LA ELIPSE

---

a = Es la distancia entre el centro de la elipse a uno de sus extremos sobre el eje mayor

b = Es la distancia entre el centro de la elipse a uno de extremos de su eje menor

c = Es la distancia del centro a uno de sus focos.

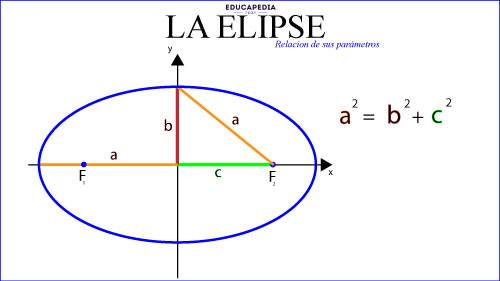
Como podemos ver en la imagen anterior, del triángulo rectángulo que trazamos y utilizando el Teorema de Pitágoras obtenemos:

a² = b² + c²

Es decir, teniendo dos valores podemos obtener el tercero. Despejando:

c² = a² – b²

b² = a² – c²

MUY IMPORTANTE:

Los valores de “a” y “b”, son los denominadores en la ecuación ordinaria de la elipse.

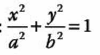
EXCENTRICIDAD DE LA ELIPSE:

---

Definimos la excentricidad de la elipse como la relación entre el parámetro “c” entre el parámetro “a”.

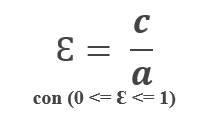
Es decir: La excentricidad de la elipse es la división de la distancia del centro a un foco (c) entre la distancia del centro a un vértice (a).

Utilizando la relación de los parámetros de la elipse, podemos obtener la excentricidad en términos de a y b.

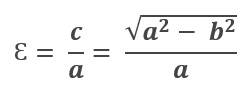
Nota:

Fíjate que ɛ puede valer entre [0, 1). Cuando ɛ = 0 es una circunferencia porque el foco estaría en el centro.

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.