PUNTOS DE INFLEXIÓN Y DE CONCAVIDAD EN UNA CURVA

PUNTO DE INFLEXIÓN

---

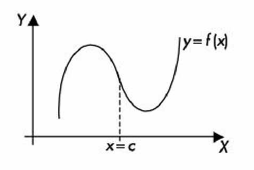
El punto de inflexión es el punto donde la función cambia de un tipo de concavidad a otra.

También se puede decir que es el punto donde la pendiente de la curva cambia de sentido.

Una función tiene un punto de inflexión en el punto “c” si:

1.-Su segunda derivada es = 0 (f´´(c) = 0)

2.-Existe cambio de concavidad

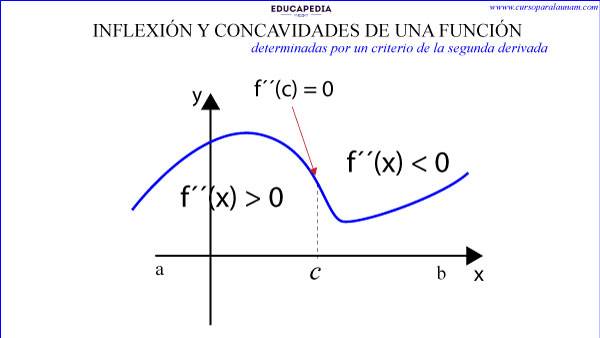
CONCAVIDAD:

---

Una función es cóncava hacia arriba en un intervalo (a, b) si:

                    Para todo x en (a, b), f´´(x) > 0.

(la segunda derivada es positiva)

Una función es cóncava hacia abajo en un intervalo (a, b) si:

                    Para todo x en (a, b), f´´(x) < 0.

(la segunda derivada es negativa)

Ejemplos de puntos de inflexión y concavidad en un función:

1.- Determinar el punto de inflexión de la siguiente función:

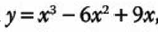
         Primero obtenemos la 2do derivada:

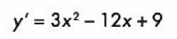
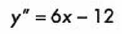
         Después, igualamos a cero y despejamos “x”:

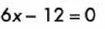
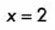
         Por ultimo analizamos valores menores y mayores a este valor:

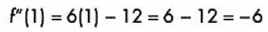
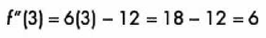
         Con esto observamos que la segunda derivada cambio de negativo a positivo en el punto x = 2, por lo tanto, tiene un punto de inflexión ahí mismo.

         Para obtener la ordenada de ese punto y completar las coordenadas de ese punto, sustituimos en la función original:

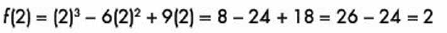
         Por lo tanto, tenemos un punto de inflexión en las coordenadas (2, 2).

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.