MÁXIMOS Y MÍNIMOS ABSOLUTOS EN UN INTERVALO CERRADO
Definición de máximos y mínimos absolutos en un intervalo cerrado
Debido a que la derivada de una función también es la pendiente de la línea tangente en ese punto, si observamos cómo va cambiando la pendiente podemos observar también los cambios que hay en la función que se estudia.
El máximo absoluto de una función es el punto con el valor más alto (f(x)) de todos los valores que tiene el dominio (x).
El mínimo absoluto de una función es el punto con el valor más pequeño (f(x)) de todos los valores que tiene el dominio (x).
Procedimiento para determinar máximo y mínimos absolutos de una función.
1.-Calcular la derivada de la función
2.-Calcular los valores para los cuales la primera derivada es = 0
3.-Con los valores calculados, los sustituimos en la función para calcular los valores de f(x)
4.-De los valores anteriores, el máximo valor f(x) (en el cual la primera derivada es cero) ese será el máximo absoluto de la función.
5.- De los valores obtenidos en el paso 3, el mínimo valor f(x) (el cual también su derivada fue cero) ese será el mínimo absoluto de la función
Ejemplos de máximos y mínimos de una función en un intervalo cerrado:
1.- Calcula el máximo y el mínimo absoluto de la siguiente función en el intervalo [-1, 5]:
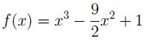
Primero derivamos la función:
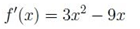
Después hayamos los puntos críticos:
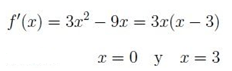
Después obtenemos los valores de la función en los extremos:
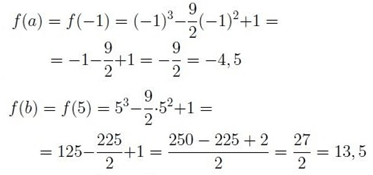
A continuación, obtenemos los valores de la función en los puntos críticos:
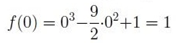
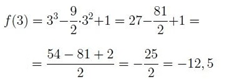
Comparando estos resultados, ya podemos determinar cuál es su máximo y su mínimo absoluto de la función en determinado intervalo:
Mínimo absoluto: (3, -12.5)
Máximo absoluto: (5, 13.5)
Como lo podemos ver en su gráfica:
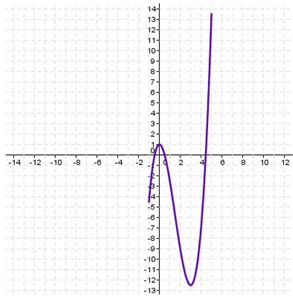
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00