GRÁFICAS Y ASÍNTOTAS DE LAS FUNCIONES EXPONENCIAL Y LOGARITMICA
RECUERDA:
La asíntota de una función es una línea recta que a la cual la grafica de la función se aproxima continuamente.
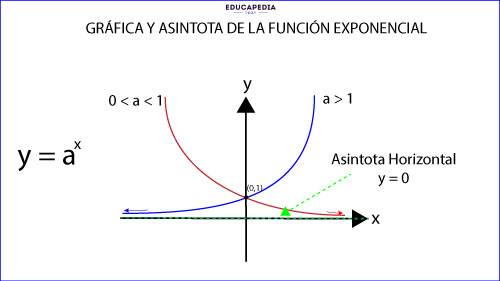
GRAFICA Y ASÍNTOTAS DE LA FUNCIÓN EXPONENCIAL:
La asíntota de la función exponencial es la recta “y = 0” que coincide con el “Eje x”.
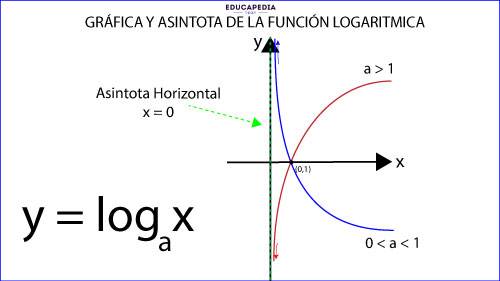
GRAFICA Y ASÍNTOTAS DE LA FUNCIÓN LOGARÍTMICA:
La asíntota de la función logarítmica, es la recta “x = 0” que coincide con el “Eje y”.
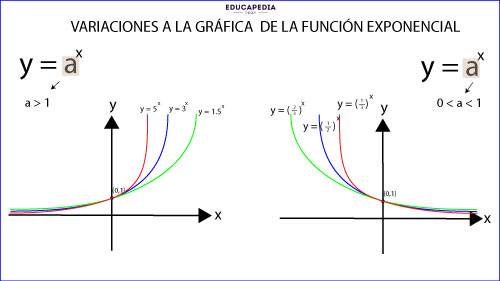
VARIACIONES A LA GRAFICA DE LA FUNCIÓN EXPONENCIAL
La primera variación que podemos realizar en la función exponencial es darle valores diferentes a la base “a”. Que como ya vimos puede variar en dos rangos: de (0, 1) y de (1, ∞).
OBSERVA:
1.- Todas la graficas pasan por el punto (0,1) porque todos los valores de “a” elevado a la “0” (cero) es igual a 1.
2.- Si la base “a” es mayor, la gráfica crece todavía más rápido.
3.- Cuando “a” es menor que 1, la gráfica se vuelve decreciente.
La otra variación que podemos tener en la grafica de la función exponencial es multiplicar y/o sumar y restar una constate a la función.
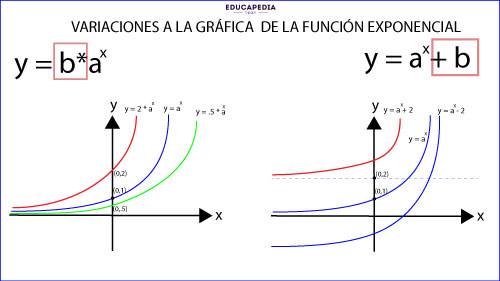
OBSERVA:
1.- Todas estas variaciones cambian el punto donde la grafica toca al eje de las ordenadas (Eje y).
2.- Si se multiplica por “b”, el punto donde tocará al eje de las ordenadas es (0, b).
3.- Si se suma o se resta “b”, el punto donde tocará al eje de las ordenadas será (0, b+1), además de que cambiara su asíntota el cual ahora será y = b.
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00