FORMAS ORDINARIA Y GENERAL DE LA ECUACIÓN DE LA PARÁBOLA CUANDO EL VÉRTICE ESTÁ EN UN PUNTO CUALQUIERA DEL PLANO Y EJE FOCAL PARALELO A ALGUNO DE LOS EJES COORDINADOS
Las formas ordinaria y general de la ecuación de la parábola con vértice en cualquier punto, pero con eje focal paralelo a algún eje coordinado son:

DETALLES DE LA ECUACIÓN DE LA PARÁBOLA CON VÉRTICE EN CUALQUIER PUNTO Y EJE FOCAL PARALELO A ALGÚN EJE COORDINADO
PARÁBOLA HORIZONTAL Y CÓNCAVA HACIA LA DERECHA
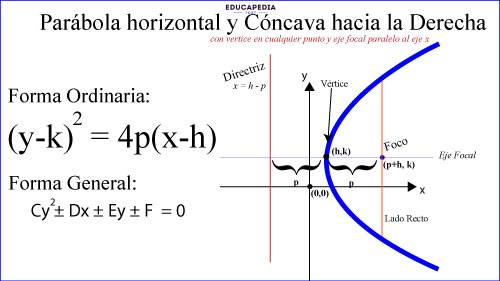


PARÁBOLA HORIZONTAL Y CÓNCAVA HACIA LA IZQUIERDA
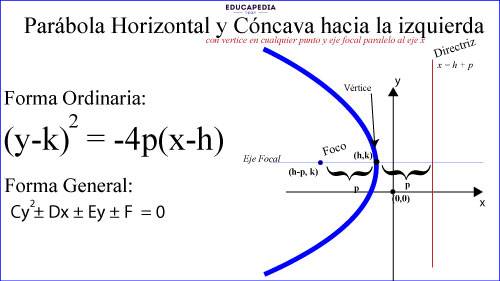

PARÁBOLA VERTICAL Y CÓNCAVA HACIA LA ARRIBA
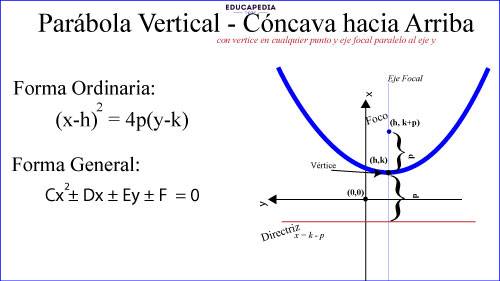

PARÁBOLA VERTICAL Y CÓNCAVA HACIA LA ABAJO
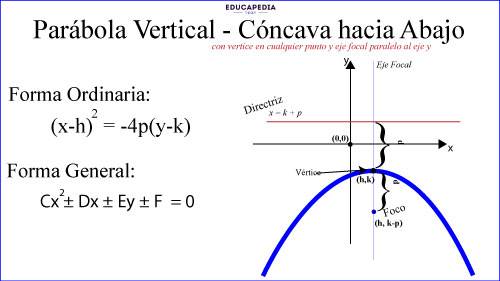

CONVERSIÓN DE LA FORMA GENERAL A LA FORMA ORDINARIA DE LA ECUACIÓN DE LA PARÁBOLA CON VÉRTICE EN CUALQUIER PUNTO
Si tenemos la ecuación de una parábola en su forma general, no podemos determinar las propiedades graficas de esta parábola hasta que la convirtamos en la forma ordinaria.
Recuerda:
Recuerda que la forma ordinaria de la parábola nos da información inmediata sobre su vértice (h, k) y sobre p, con lo cual podemos calcular rápidamente el foco y la directriz de la parábola.
Ejemplo:
Convertir la ecuación de la siguiente parábola en forma ordinaria:
4×2 – 20x – 24y + 97 = 0
1.- Despejamos la variable al cuadrado
2.- Formamos el trinomio al cuadrado perfecto
3.- Agrupamos términos y los expresamos en forma ordinaria.
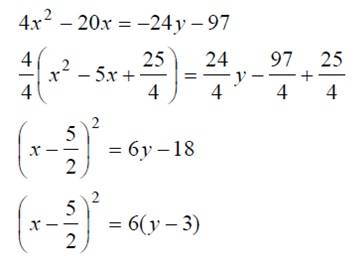
Con lo cual podemos concluir que:
Vértice: (5/2, 3)
Eje focal: Paralelo a al eje y
La parábola es cóncava hacia arriba
Foco: (5/2, 9/2)
P= 3/2 debido a que 6 = 4p
Directriz: y = 3/2
Y su grafica es la siguiente:
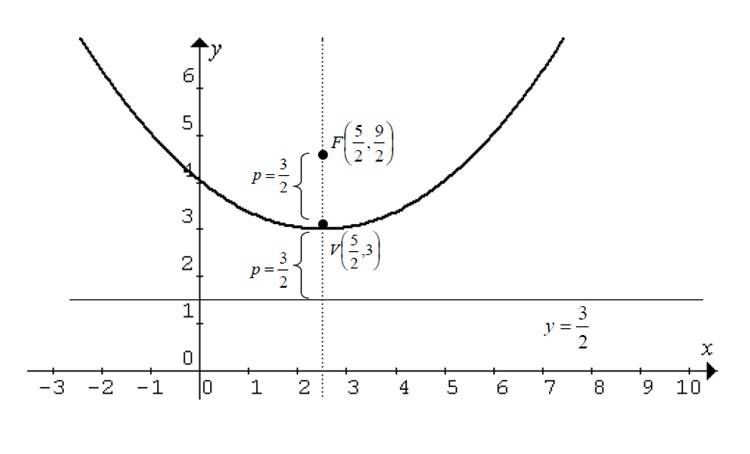
HALLAR LA FORMA GENERAL DE LA ECUACIÓN DE LA PARÁBOLA A PARTIR DE CIERTOS DATOS INICIALES.
En este tipo de problemas, regularmente nos proporcionan los datos del vértice, el foco o la directriz y con estos datos debemos crear la forma general de la ecuación de la parábola.
Ejemplo:
Encuentra la ecuación de la parábola en su forma general teniendo como datos iniciales: Foco: (-3, -2) y directriz: x = 1.
1.- Para ayudarnos a identificar el tipo de parábola podemos graficarla con los datos dados:
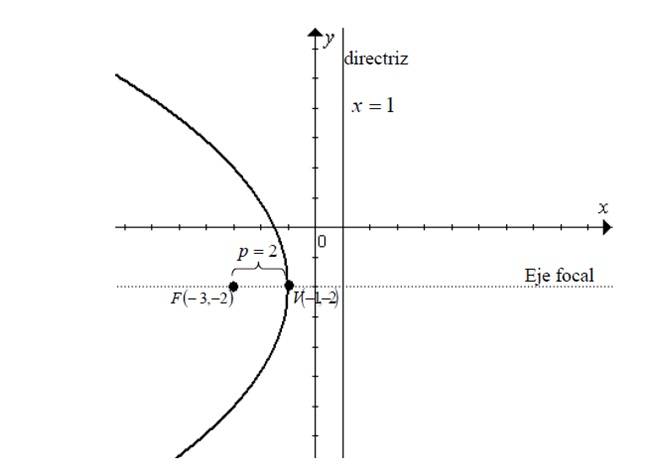
Con esto podemos identificar:
El vértice: (-1, -2)
El eje focal es paralelo al eje x
La parábola es cóncava hacia la izquierda
P = 2
Sustituimos estos valores en la forma ordinaria de una parábola horizontal cóncava hacia la izquierda y con vértice en cualquier punto.
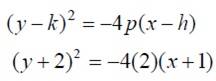
Por último, realizamos las operaciones agrupadas y la expresamos en forma general:
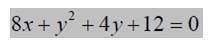
Ejemplos de la ecuación de la parábola cuando el vértice esta en cualquier punto:
1.- Determinar las coordenadas del vértice de la parábola:
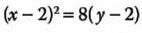
Recordemos que la parábola
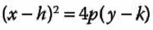
Tiene vértice en:
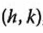
Por lo que debemos hacer la siguiente sustitución:
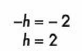
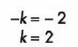
Y las coordenadas del vértice son: (2, 2)
O simplemente recuerda que en la ecuación de la parábola con vértice en (h, k), tienen signos contrarios a las coordenadas del vértice.
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00







