ECUACIONES DE LA TANGENTE Y DE LA NORMAL A UNA CURVA
Como recordaras, todas las líneas rectas están representadas por ecuaciones lineales y tal como vimos en el capítulo la recta, para poder obtener la ecuación de una línea recta podemos utilizar la forma de la ecuación “punto-pendiente”.
Con esto y utilizando la derivada para calcular la pendiente podemos obtener la ecuación de la tangente o la normal.
OBTENCIÓN DE LA ECUACIÓN DE LA TANGENTE EN CIERTO PUNTO
1.-Utilizamos la ecuación de la recta punto-pendiente
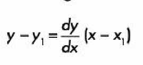
2.-En este caso, la pendiente es la derivada de la función de la cual obtendremos su tangente
3.-Se obtiene la derivada de la función en cuestión y se evalúa en el punto dado, para obtener la pendiente de la recta tangente.
4.-Se sustituye el punto dado y la pendiente obtenida en la ecuación de la línea punto-pendiente
5.-Se simplifica lo más que se pueda y esa será la ecuación de la tangente.
OBTENCIÓN DE LA ECUACIÓN DE LA NORMAL A LA CURVA
Para obtener la normal de la curva, se aplica el mismo procedimiento anterior, pero cuando sustituimos la pendiente que obtuvimos de la derivada de la función, aplicamos la condición de perpendicularidad para que la ecuación que obtengamos sea perpendicular a la tangente.
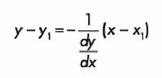
Ejemplos de ecuación de la tangente y la normal a una curva:
1.- Determina la ecuación de la recta tangente y la recta normal a la siguiente función en el punto (1, 4):
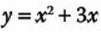
Primero obtenemos la derivada de esta función:
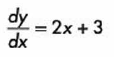
Después sustituimos el valor de “x” deseado, para obtener el valor de la derivada en ese punto:
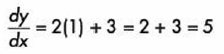
Ya conociendo la pendiente y el punto, construimos la ecuación de esta recta tangente, hasta llegar a su forma general.
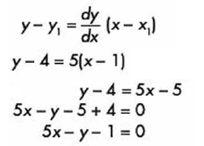
Utilizando la misma ecuación punto-pendiente pero ahora con pendiente inversa negativa para obtener su normal, obtenemos:
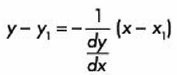
Sustituyendo:
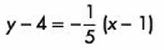
Y, por último, simplificamos y obtenemos:
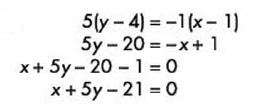
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00