MÁXIMOS Y MÍNIMOS RELATIVOS DE UNA FUNCIÓN
Definición de máximos y mínimos relativos de una función
Debido a que la derivada de una función también es la pendiente de la línea tangente en cada punto de la función, si observamos cómo va cambiando está pendiente podemos conocer los cambios que hay en la función.
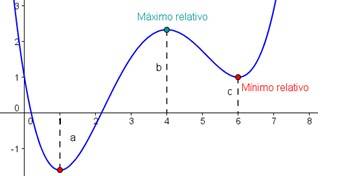
El máximo relativo de una función es el punto con el valor más alto (f(x)) en un segmento de la curva.
El mínimo relativo de una función es el punto con el valor más pequeño (f(x)) en un segmento de la curva.
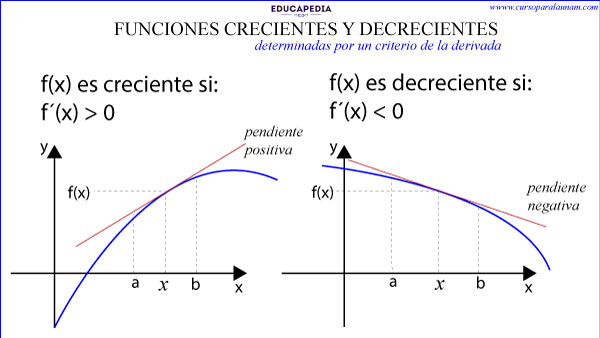
FUNCIONES CRECIENTES Y DECRECIENTES DETERMINADAS POR UN CRITERIO DE LA DERIVADA
Para determinar si una función es creciente o decreciente en un intervalo utilizamos el siguiente criterio de la derivada:
FUNCIÓN CRECIENTE
Si función f(x) es creciente en el intervalo (a, b) si f´(x) > 0 para todo x en (a, b).
Es decir, en ese intervalo, todas las derivadas de los puntos de ese intervalo son positivas, o lo que es lo mismo, todas las pendientes de las rectas tangentes a esos puntos son positivas.
FUNCIÓN DECRECIENTE
Si función f(x) es decreciente en el intervalo (a, b) si f´(x) < 0 para todo x en (a, b).
Es decir, en ese intervalo, todas las derivadas de los puntos de ese intervalo son negativas, o lo que es lo mismo, todas las pendientes de las rectas tangentes a esos puntos son negativas.
CRITERIOS PARA DETERMINAR MÁXIMO Y MÍNIMO RELATIVOS DE UN FUNCIÓN
Si ya sabemos determinar si una función es creciente o decreciente utilizando un criterio de la derivada, juntando los dos criterios podemos determinar cuándo tiene un “crece-decrece” (un máximo) o un “decrece-crece” (un mínimo).
CRITERIO DE LA PRIMERA DERIVADA:
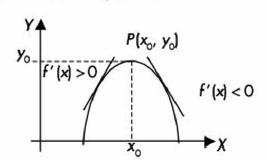
La función y = f(x) tiene un punto máximo en (x0, y0) si:
La derivada de f(x0) = 0
Antes de x0 la derivada es positiva
Después de x0 la derivada es negativa
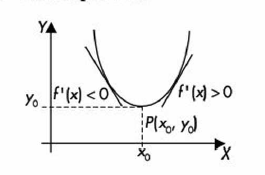
La función y = f(x) tiene un punto mínimo en (x0, y0) si:
La derivada de f(x0) = 0
Antes de x0 la derivada es negativa
Después de x0 la derivada es positiva
CRITERIO DE LA SEGUNDA DERIVADA:
La función y = f(x) tiene un punto máximo en (x0, y0) si:
La derivada de f(x0) = 0
La segunda derivada es < 0 (negativa)
La función y = f(x) tiene un punto mínimo en (x0, y0) si:
La derivada de f(x0) = 0
La segunda derivada es > 0 (positiva)
Ejemplos de máximos y mínimos relativos de una función:
1.- Determina que tipo de punto (maximo o minimo) tiene la siguiente funcion y que coordenadas tiene:
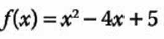
Primero se obtiene al primera derivada:
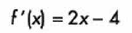
Despues igualamos a cero y despejamos “x”:
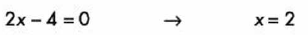
Despues analizamos que pasa con la derivada antes y despues de este punto:
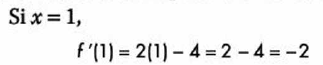
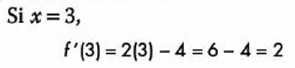
Debido a que antes del punto la derivada es negativa y después del punto la derivada es positiva, concluimos que tiene un punto mínimo en x = 2.
Por último, sustituimos este valor en la función original, para que nos de la coordenada del punto donde tiene el punto mínimo.
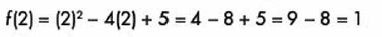
Por lo tanto, la coordenada del punto mínimo es (2, 1)
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00







