MÉTODOS DE SOLUCIÓN PARA SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS
Para resolver un sistema de dos ecuaciones con dos incógnitas se pueden utilizar varios métodos. Sin embargo, antes de intentar resolverlas, debemos saber qué tipo de solución tiene el sistema.
TIPOS DE SOLUCIONES A UN SISTEMA DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS
Un sistema de dos ecuaciones lineales con dos incógnitas puede tener 3 tipos de soluciones:
1.-Una solución: Son los sistemas que solo tienen una solución y donde se tiene que encontrar el valor de “x” y de “y”. Es decir, solo un par de valores resolverá las dos ecuaciones
2.-Una infinidad de soluciones: Existen sistemas que tienen infinidad de soluciones cuando una ecuación del sistema se puede obtener por la multiplicación o división de un numero por la otra ecuación del sistema, entonces las dos ecuaciones son equivalentes.
3.-No tienen soluciones: Si A/A1 = B/B1 = k y C/C1 es diferente de k
REPRESENTACIÓN GEOMÉTRICA DE UN SISTEMA DE DOS ECUACIONES LINEALES
La representación geométrica de las ecuaciones nos ayuda a visualizar los valores que puede tener una ecuación y en un sistema de ecuaciones nos ayuda a visualizar la solución de este sistema.
En términos geométricos, cada ecuación representa una línea en el plano cartesiano.
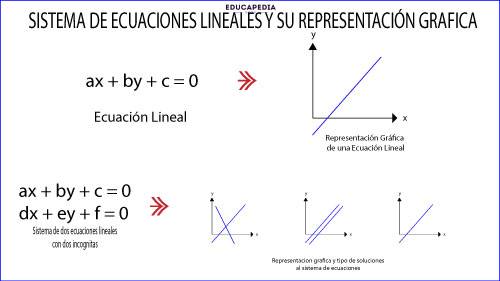
REPRESENTACIÓN GRAFICA DE LOS TIPOS DE SOLUCIONES
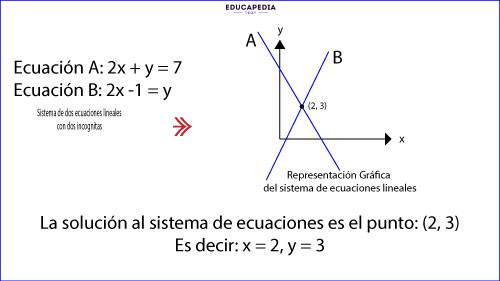
1.-Si son líneas diferentes, en algún punto se cruzan y ese punto representa la solución al sistema de 2 ecuaciones (x, y)
Es decir: “los valores del punto se pueden sustituir en las ecuaciones y conservan la igualdad (la resuelven).
2.-Si son la misma línea, tendrán una infinidad de soluciones, ya que son ecuaciones semejantes.
Si una de las ecuaciones es resultado de multiplicar o dividir por un número a la otra, entonces ambas ecuaciones representan a la misma línea.
3.-Si son dos líneas diferentes pero paralelas, están no tendrán solución, ya que geométricamente no tienen un punto donde se intercepten.
Para saber si son rectas paralelas, se tienen que cumplir los dos criterios siguientes:
1.- La división de los coeficientes de x es iguala a la división de los coeficientes de y
2.- Y si la división de los coeficientes independientes es diferente.
Ejemplos de solución de sistemas de dos ecuaciones lineales con dos incógnitas:
1.-
2.- Determinar si
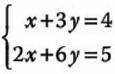
a) Se corta en (1,1)
b) Representan a la misma línea
c) Son rectas paralelas
Para verificar si se cortan en (1,1) se sustituye en las dos ecuaciones para ver si la resuelve:

Debido a que en la segunda ecuación No se conserva la igualdad, podemos decir que las líneas que representan estas ecuaciones no se cortan en el punto (1,1)
Para verificar si las dos ecuaciones representan la misma línea, tratamos de obtener una en términos de la otra multiplicada por un número, el 2 y obtenemos:
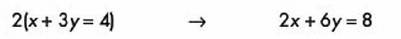
Como puedes ver, NO se pudo obtener de la primera, por lo que podemos decir que no representan a la misma línea,
Y por último para ver si son rectas diferentes pero paralelas verificamos i la división de los coeficientes de las variables x, y “y” son iguales y si la división de los coeficientes independientes es diferente.
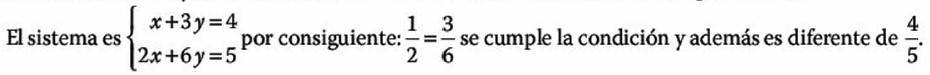
Con esto podemos concluir que las rectas representadas por el sistema de ecuaciones propuesto son paralelas.
Después de haber conocido las posibilidades de solución y su representación geométrica, podemos utilizar alguno de los siguientes métodos para resolver el sistema.
MÉTODOS DE SOLUCIÓN DE SISTEMAS DE ECUACIONES LINEALES CON DOS INCÓGNITAS:
Los métodos de solución para sistemas de ecuaciones lineales son:
1.- Regla de Cramer o Método por determinantes
2.- Método de Reducción o de suma y resta:
3.- Método por sustitución:
REGLA DE CRAMER O POR DETERMINANTES
DEFINICIÓN DE UN DETERMINANTE
Un determinante es un arreglo especial de los coeficientes de un sistema de ecuaciones lineales.

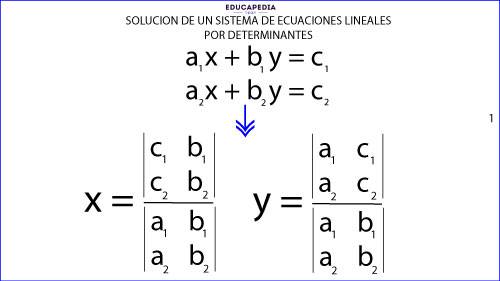
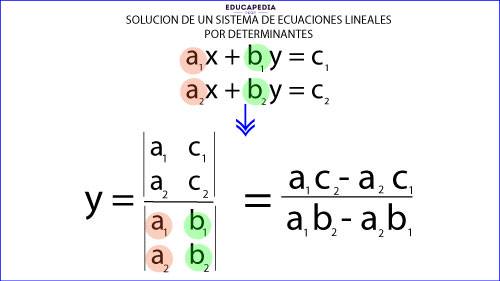
PARA RESOLVER EL SISTEMA DE ECUACIONES LINEALES POR REGLA DE CRAMER O POR DETERMINANTES
Para obtener el valor de “x” dividimos el determinante de “x” entre el determinante del sistema.
Para obtener el valor de “y” dividimos el determinante de “y” entre el determinante del sistema.
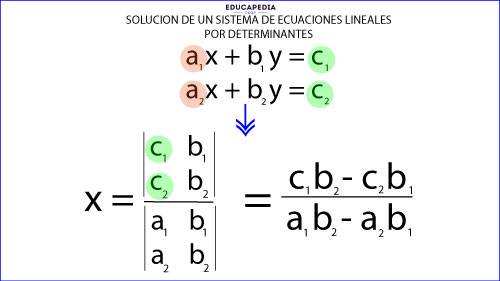
El determinante de “x” se obtiene sustituyendo los coeficientes de la variable “x” por el coeficiente “c”
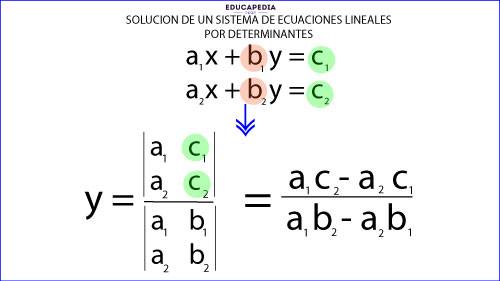
El determinante de “y” se obtiene sustituyendo los coeficientes de la variable “y” por el coeficiente “c”
El determinante del sistema se obtiene con los coeficientes de las variables “x” y “y”.
Ejemplos de solución de sistemas de dos ecuaciones lineales con dos incógnitas (utilizando la Regla de Cramer):
1.- Resolver el siguiente sistema de ecuaciones:
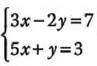
Sustituimos los coeficientes en nuestros determinantes:

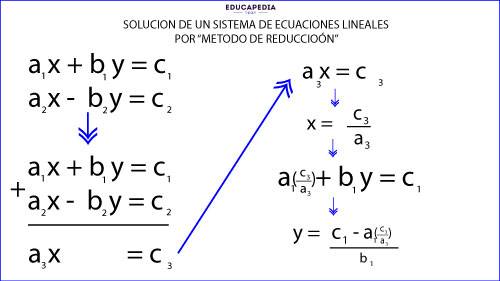
MÉTODO DE REDUCCIÓN O DE SUMA Y RESTA
PROCEDIMIENTO:
1.- Eliminar una de las variables al sumar las dos ecuaciones y obtener una ecuación de primer grado con una variable
2.- Despejar esta variable y así obtener su valor.
3.- Después este valor se sustituye en cualquiera de las dos ecuaciones y se obtiene el valor de la otra variable.
Ejemplos:
1.- Encontrar el valor de las variables en el sistema:
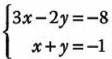
Antes de sumarlas o restarlas, a la segunda ecuación se multiplica por 2 para que podamos eliminar un elemento de la primera ecuación:
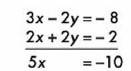
De aquí obtenemos:
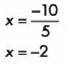
Este valor se sustituye en cualquier de las dos ecuaciones para obtener el otro valor:
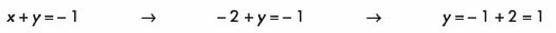
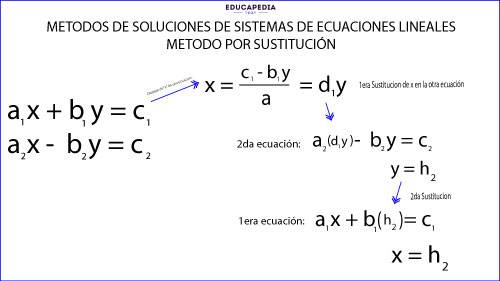
MÉTODO POR SUSTITUCIÓN
En este método:
1.- Se elige una ecuación para despejar una de sus incógnitas
2.- Se sustituye en la otra ecuación, de esta manera se obtiene una ecuación de primer grado con una incógnita.
3.- En esta ecuación se despeja la incógnita y se obtiene su valor.
4.-Por último, este valor se sustituye en la otra ecuación y se obtiene el valor de la otra incógnita.
Ejemplos:
1.- Resuelve el siguiente sistema por sustitución:
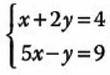
De la primera ecuación despejamos x:
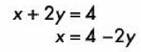
Y la sustituimos en la segunda ecuación:
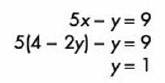
Con este valor lo sustituimos en el despeje de x:
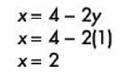
Con lo cual obtenemos las dos incógnitas:
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00







