MÉTODOS DE SOLUCIÓN (REGLA DE CRAMER) PARA SISTEMAS DE TRES ECUACIONES LINEALES CON TRES INCOGNITAS

Definición de sistema de tres ecuaciones lineales con tres incógnitas

Un sistema de 3 ecuaciones con 3 incógnitas, tiene la forma siguiente:

a₁x + b₁y + c₁z = d₁

a₂x + b₂y + c₂z = d₂

a₃x + b₃y + c₃z = d₃

Para resolver este tipo de sistemas de ecuaciones lineales se utiliza el método por determinantes:

Según el método por determinantes, la solución a este sistema está dada por:

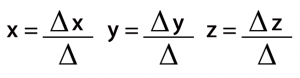
Donde:

 Δx es el determinante de x

 Δy es el determinante de y

  Δz es el determinante de z

  Δ es el determinante del sistema.

Métodos de solución para sistemas de tres ecuaciones lineales con tres incógnitas.

Para obtener los valores de los determinantes existen 2 forma de realizar las operaciones en los arreglos:

1era forma: REGLA DE SARRUS: Extensión de coeficientes en los arreglos

2da forma: REGLA DE CRAMER: Operaciones triangulares en los arreglos

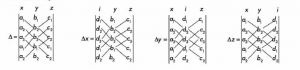
1ERA FORMA PARA RESOLVER DETERMINANTES: REGLA DE SARRUS: EXTENSIÓN DE COEFICIENTES EN LOS ARREGLOS.

1.- Los coeficientes se colocan de manera vertical según como están en el sistema de tres ecuaciones.

2.- Se repiten los dos primeros renglones del arreglo después de los 3 renglones correspondientes a las 3 ecuaciones.

3.- Para obtener el valor de una variable, se sustituyen sus coeficientes por los coeficientes “c” o los que no están relaciones a ninguna variable.

4.- El determinante del sistema es aquel en la que sus coeficientes son los coeficientes de las variables en cuestión. Es decir, en este determinante no se utilizan los coeficientes “c”.

5.- El resultado de las operaciones son: La suma de las multiplicaciones en diagonales ( \ ) menos la suma de las multiplicaciones en diagonales ( / ).

Gráficamente se realizan de la siguiente manera:

Ejemplos de solución de sistema de tres ecuaciones lineales con tres incógnitas:

1.- Resuelve el siguiente sistema de ecuaciones:

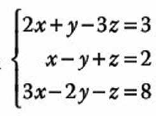
Primero calculamos el determinante del sistema:

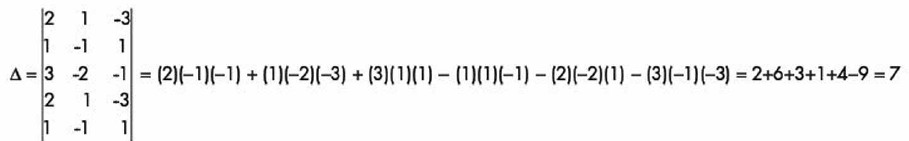
Después calculamos el determinante de “x”:

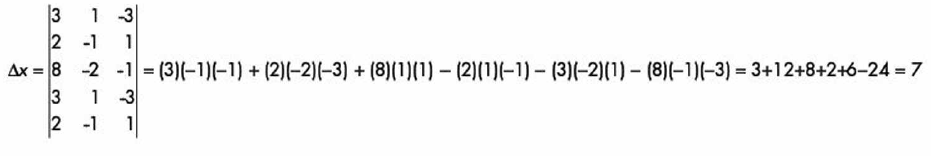
Por lo que tenemos que el valor de x:

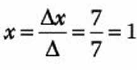
Continua con el cálculo de “y” y “z”.

2DA FORMA PARA RESOLVER DETERMINANTES: REGLA DE CRAMER: EXTENSIÓN DE COEFICIENTES EN LOS ARREGLOS.

Sin agregar los coeficientes como en la manera anterior, podemos hacer el siguiente método.

El determinante de una matriz de 3 x 3 es:

1.-La suma de sus productos diagonales

2.-menos la resta de sus productos diagonales inversos.

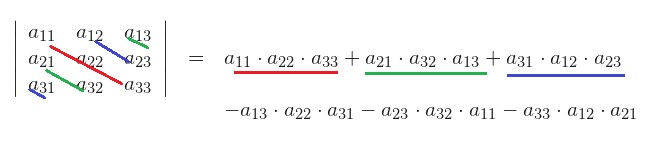
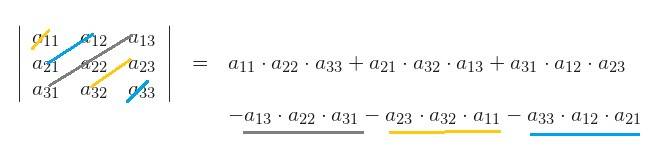
Para calcular el determinante del sistema:

          Los coeficientes serán los de las variables

Para calcular el determinante de alguna variable:

          Los coeficientes de esa variable serán sustituidos por los coeficientes independientes

Ejemplos de soluciones de tres ecuaciones lineales con tres incognitas:

1.- Resuelve el siguiente sistema de ecuaciones lineales:

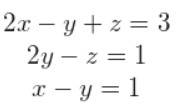
Primero calculamos el determinante del sistema

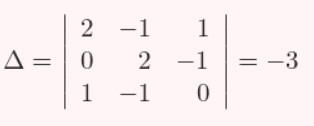
Después calculamos el valor de “x”:

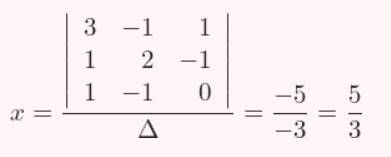
Después calculamos el valor de “y”:

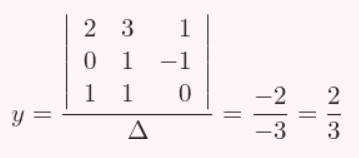
Después calculamos el valor de “z”:

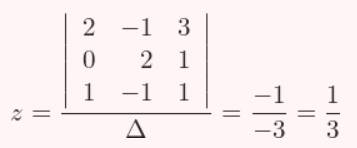
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.