LEY DE LOS SENOS Y LEY DE LOS COSENOS

Como vimos en el capítulo anterior, para resolver problemas con triángulos rectángulos usamos básicamente el Teorema de Pitágoras y las identidades trigonométricas.

Pero cuando el triángulo a resolver no es rectángulo, es decir, no tiene un ángulo de 90 grados, no podemos aplicar el Teorema del Pitágoras.

Así que para triángulos que no son rectángulos, podemos usar la Ley de los Senos y la Ley de Cosenos para encontrar el valor de algún ángulo o de algún lado, conociendo los demás valores.

LEY DE LOS SENOS

---

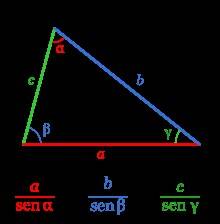
La Ley de los Senos establece que la división de un lado de un triángulo entre el seno del ángulo opuesto a ese lado, es igual a todas las divisiones de los demás lados con sus respectivos ángulos.

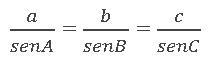
LEY DE LOS COSENOS:

---

La Ley de los Cosenos establece que el cuadrado de un lado de un triángulo es igual a la suma de los cuadrados de los lados restantes, menos el doble producto de dichos lados por el coseno del ángulo opuesto al lado buscado.

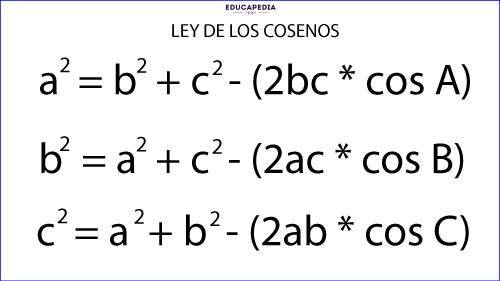
Por supuesto, despejando tenemos que:

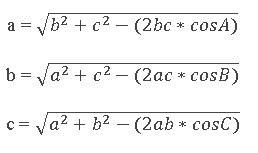
Y si necesitamos encontrar el valor de algún ángulo con la Ley de los Cosenos podemos expresarlo así:

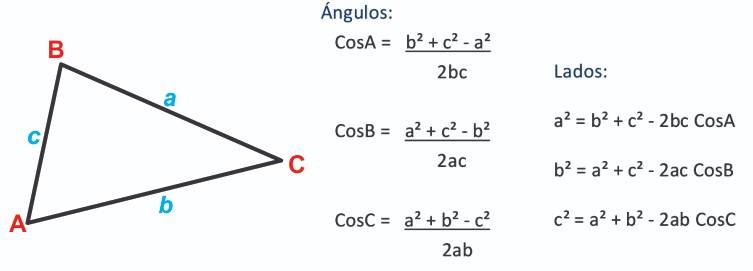
¡IMPORTANTE!

En realidad, solo necesitas recordar una sola formula y saber despejar correctamente.

EJEMPLOS DE LA LEY DE LOS SENOS:

1.- Encuentra el valor de lado “a” del siguiente triangulo:

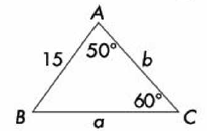
         Aplicando la Ley de los Senos tenemos:

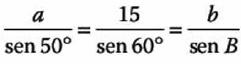
         Tomando la primera igualdad tenemos:

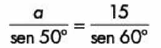
         Y despejando obtenemos:

EJEMPLOS DE LA LEY DE LOS COSENOS:

1.- Encuentra el valor del lado “c” en el siguiente triangulo:

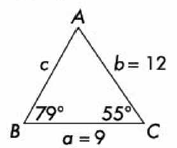
         Primero escogemos la fórmula que nos dará el lado que estamos buscando:

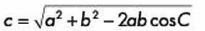
         Y por último sustituimos los valores correspondientes:

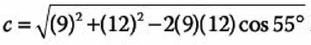
         Realiza las operaciones para obtener el valor de “c”.

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.