CRITERIOS PARA IDENTIFICAR A LA CÓNICA QUE REPRESENTA UNA ECUACIÓN DE SEGUNDO GRADO
Conociendo las formas ordinarias o canónicas de las cónicas, ya podemos distinguir que cónica representa cierta ecuación.
Pero en el caso de que la ecuación no esté en forma ordinario y sea de la forma general tenemos que utilizar ciertos criterios para identificarla.
Dada la ecuación general de segundo grado:
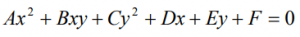
Utilizamos los siguientes criterios:
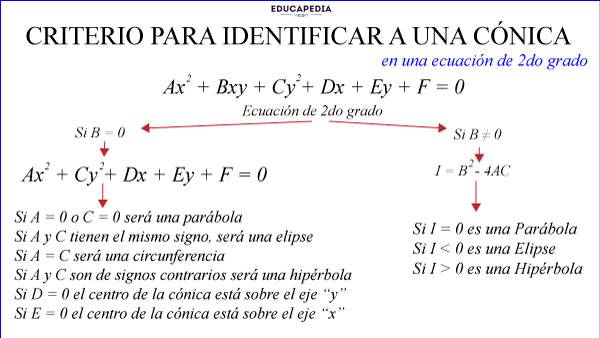
CRITERIOS PARA IDENTIFICAR LA FORMA DE LA CÓNICA EN LA ECUACIÓN GENERAL DE SEGUNDO GRADO
Si B = 0, nuestra ecuación general será de la forma:
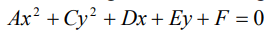
Aplicamos los siguientes criterios para saber que cónica representa:
1.- Si A = 0 o C = 0 será una parábola
2.-Si A y C tienen el mismo signo, será una elipse
3.-Si A = C será una circunferencia
4.-Si A y C son de signos contrarios será una hipérbola
5.-Si D = 0 el centro de la cónica está sobre el eje “y”
6.-Si E = 0 el centro de la cónica está sobre el eje “x”
MUY IMPORTANTE
Cuando B = 0, es decir, cuando no existe el término “xy”, los ejes de estas cónicas son paralelos a los ejes coordenados x, y.
Cuando B ≠ 0, nuestra ecuación regresa a la forma general:
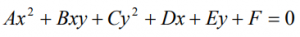
Y tenemos que aplicas otros criterios para determinar el tipo de cónica que representan.
En este caso, el discriminante es:
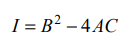

Ejemplos para identificar una cónica en una ecuación de 2do grado:
1.- Determina qué tipo de cónica representa la siguiente ecuación:
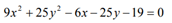
Primero vemos que tipo de caso es:
Como B = 0 entonces aplicamos los primeros criterios, así que:
Como A = 9 y C = 25 y tienen el mismo signo, entonces representa una ELIPSE.
Además, sus ejes son paralelos a los ejes “x” y “y”.
Por otra parte, como sus coeficientes D = -6 y E = -25 nos indican que su centro está fuera del origen.
Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.
-
 Guía UNAM Área 4 2023Producto rebajado$450.00
Guía UNAM Área 4 2023Producto rebajado$450.00 -
 Guía UNAM Área 3 2023Producto rebajado$450.00
Guía UNAM Área 3 2023Producto rebajado$450.00 -
 Guía UNAM Área 2 2023Producto rebajado$450.00
Guía UNAM Área 2 2023Producto rebajado$450.00 -
 Guía UNAM Área 1 2023Producto rebajado$450.00
Guía UNAM Área 1 2023Producto rebajado$450.00







