DOMINIO Y RANGO DE LAS FUNCIONES TRIGONOMETRICAS DIRECTAS

Recuerda:

El dominio de una función es el conjunto de valores que puede tener “x” y el rango de una función es el conjunto de valores que adquiere “y” dependiendo de la función. Es decir, después de realizarle las operaciones a “x” que nos indique la función.

DOMINIO Y RANGO DE LA FUNCIÓN SENO:

---

Dominio: (-∞, ∞)

Rango: [-1, 1]

Véase la siguiente imagen:

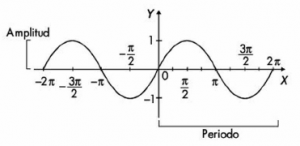
Recuerda

Esta grafica nace de los valores del círculo trigonométrico; el lado derecho de la gráfica corresponde a los valores del ángulo que va creciendo en sentido contrario a las manecillas del reloj; comienza desde cero y crece hasta el infinito (ojo: esto significa, que el ángulo le puede dar muchas vueltas al triangulo trigonométrico, por eso su valor puede crecer hasta el infinito).

El lado izquierdo de la gráfica corresponde a los valores del ángulo que se mueve en sentido de las manecillas del reloj.

El rango, por definición del círculo trigonométrico, puede variar de -1 a 1, ya que el circulo tiene radio 1.

DOMINIO Y RANGO DE LA FUNCIÓN COSENO:

---

Dominio: (-∞, ∞)

Rango: [-1, 1]

Véase la siguiente imagen:

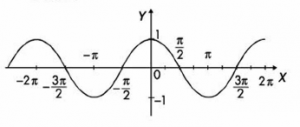
OJO:

El dominio y el rango es exactamente el mismo en la función seno y coseno. Lo que varía es el valor que el corresponde a cada ángulo, pero todos los valores estarán en el mismo rango [-1, +1].

Observa las gráficas de seno y coseno y determina las diferencias:

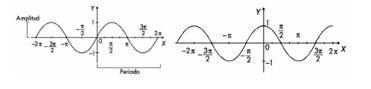
DOMINIO Y RANGO DE LA FUNCIÓN TANGENTE:

---

Dominio: (todos los reales excepto: x = ))

Rango: (-∞, ∞)

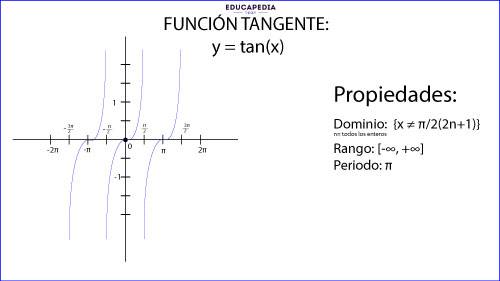
Nota: El dominio de la función tangente son todos los números reales excepto cuando cos θ = 0, porque es el denominador de la función tangente y porque la división entre cero es un valor indeterminado (infinito)

Mas ejemplos, ejercicios y preguntas clave de examen, en nuestras guías digitales.